一个复数不等式
一个复数不等式:
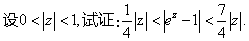
复变函数复数的不等式001.gif
Let [latex]0<\mid z\mid <1[/latex],please proof :
[latex]\frac{1}{4}\mid z\mid<\mid e^z-1\mid<\frac{7}{4}\mid z\mid[/latex]
[ Last edited by Edstrayer on 2014-4-29 at 19:35 ]
今日热帖
一个复数不等式:
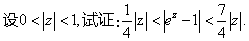
复变函数复数的不等式001.gif
Let [latex]0<\mid z\mid <1[/latex],please proof :
[latex]\frac{1}{4}\mid z\mid<\mid e^z-1\mid<\frac{7}{4}\mid z\mid[/latex]



嗯,是的,我错了
这个题目不需要用数学软件计算吧?
数学软件让我们看到要证明的不等式是:
(1- e^{-1}) |z| < |e^z -1| < (e-1) |z|, 当 |z| <1 时.
然而 the more I see, the less I know.
我证明不了上面的不等式, 想请教高明能否写出严格证明.
这只要用幂级数e^z=\sum\limits_{n=0}^{+\infty}\frac{z^n}{n!}代入\mid e^-1\mid中后用三角不等式进行放缩就可以得到所要证明的不等式。
我知道怎么证明 |e^z-1| < (e-1) |z|, 我想知道的是怎么证明
|e^z -1| > (1- e^{-1}) |z|.
我不想要 |e^z-1| > (3-e) |z| 这样粗放的估计, 因为 3-e=0.2817..,
1-e^{-1} =0.632 差的非常多.
当0<x<1时,
|e^x-1|=\sum_{n=1}^{+\infty}\frac{x^n}{n!}
=x \sum_{n=1}^{+\infty}\frac{x^{n-1}}{n!}
=x(1+\sum_{n=2}^{+\infty}\frac{x^{n-1}}{n!})
>=x(1-(\sum_{n=2}^{+\infty}\frac{x^{n-1}}{n!}))
>x(1-(\sum_{n=2}^{+\infty}\frac{1}{n!}))
=x(3-e)
这里当x→1时,\sum_{n=2}^{+\infty}\frac{x^{n-1}}{n!}→\sum_{n=2}^{+\infty}\frac{1}{n!}=e-2
所以不等式|e^z-1|>(3-e)|z|不能改进为|e^z-1|>(1-1/e)|z|
不妨检查一下逻辑:
|e^x-1| >= x *(...).
当 x--> 1 时, (...) =e-2, 然后 你说:
所以 不等式不能改进. 这有点风马牛不相及啊.
顶多说, 用你所述的放缩法, 不等式所能达到的最好程度.
定理: 当 |z|<1时, |e^z -1| > (1-e^{-1}) |z|. 求证明. (由图形可知, 定理成立)
,
实数的情形都不能改进,复数更不能够,你所说的命题不成立