一个复数不等式
一个复数不等式:
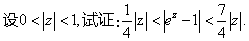
复变函数复数的不等式001.gif
Let [latex]0<\mid z\mid <1[/latex],please proof :
[latex]\frac{1}{4}\mid z\mid<\mid e^z-1\mid<\frac{7}{4}\mid z\mid[/latex]
[ Last edited by Edstrayer on 2014-4-29 at 19:35 ]
今日热帖
一个复数不等式:
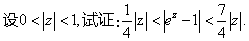
复变函数复数的不等式001.gif
Let [latex]0<\mid z\mid <1[/latex],please proof :
[latex]\frac{1}{4}\mid z\mid<\mid e^z-1\mid<\frac{7}{4}\mid z\mid[/latex]



取z=x+iy
转变成 实函数 sqrt((exp(2*x)-2*exp(x)*cos(y)+1)/(x^2+y^2)) 求极值?
不对。e^z-1的值为:
1.png
编辑:上面的内容是错的,2楼的是对的
,
用求极值的方法不好解吧?
这个不等式可以改进为:
设0<\mid z\mid<1,试证:
(3-e)\mid z\mid<\mid e^z-1\mid<(e-1)\mid z\mid.
我觉得应该对于|e^z-1|^2,先变换,再展开。
把(siny)^2换为1-(cosy)^2,把(cosy)^2换为(cos2y+1)/2,
再把e^(2x),e^x,cosy按照麦克劳林级数展开。
接下来的处理就看你了
考虑到 解析函数 f(z)=(e^z-1)/z 的最大值和最小值只在边界 |z|=1上取到, 因此画了两个图: 一个是 (e^z-1)的图像, with |z|=1 (红色), 另一个是模 |e^z-1| (蓝色). 貌似 min=1-e^{-1}, max=e-1.哪位大神能严格证明之?

Matlab 源程序:
N=500; th = 0:pi/N:2*pi;
a =exp(cos(th)).*cos(sin(th))-1;
b =exp(cos(th)).*sin(sin(th));
c =sqrt(a.^2 +b.^2);
plot( a, b, 'r', th, c,'b')
Emuch007.png
单独出一项sin^2(y) 有问题。