小木虫

当前位置：首页 > 数学 >一个代数恒等式的证明

一个代数恒等式的证明

作者 Edstrayer: 来源: 小木虫 350 7 举报帖子

题目：设x，y，z是正实数，且满足[latex]xy+yz+zx=1[/latex]，试证：

[latex]xyz(x+y)(y+z)(z+x)-(1-x^2)(1-y^2)(1-z^2)=\frac{1}{2}\left((1-x^2)(y-z)^2+(1-y^2)(z-x)^2+(1-z^2)(x-y)^2\right)[/latex]

今日热帖

精华评论

0404600213

$xyz(x&plus;y)(y&plus;z)(x&plus;z)-(1-x^2)(1-y^2)(1-z^2)=(xz&plus;yz)(xy&plus;xz)(xy&plus;yz)-(1-x^2)(1-y^2)(1-z^2)=(1-xy)(1-xz)(1-yz)-(1-x^2)(1-y^2)(1-z^2)=x^2&plus;y^2&plus;z^2-xy-xz-yz-(x^2y^2&plus;x^2z^2&plus;y^2z^2-xy^2z-x^2yz-xyz^2)=\frac{(x-y)^2}{2}&plus;\frac{(y-z)^2}{2}&plus;\frac{(x-z)^2}{2}-\frac{(xy-xz)^2}{2}-\frac{(xz-yz)^2}{2}-\frac{(xy-yz)^2}{2}=....$ ，
Edstrayer

引用回帖:
2楼: Originally posted by 0404600213 at 2016-06-06 17:21:29
https://latex.codecogs.com/gif.l ... mp;amp;plus;z)-(1-x^2)(1-y^2)(1-z^2)=(xz&plus;yz)(xy&plus;xz)(xy&plus;yz)-(1-x^2)(1-y^2)(1-z^2)=(1-xy)(1-xz)(1-yz)-(1-x^ ...

要进一步地证明不等式：

[latex](1-x^2)(y-z)^2+(1-y^2)(z-x)^2+(1-z^2)(x-y)^2\geqslant 0[/latex]

该如何证明呢？
0404600213

暂时只能证明x,y,z至多只有一个大于1

另外约束条件可以配方成
(x+y-z)2+(x-y+z)2+(x-y-z)2=2
hank612

引用回帖:
4楼: Originally posted by 0404600213 at 2016-06-07 09:26:25
暂时只能证明x,y,z至多只有一个大于1

另外约束条件可以配方成
(x+y-z)2+(x-y+z)2+(x-y-z)2=2

你其实无意中已经说出答案了阿

如果有两个大于1，比如x,y, 那么 x 乘以 y 已经大于1。

如果恰好只有一个大于1，那么恒等式左边是一个正数减去一个负数，自然大于0

如果三个都小于1，那么恒等式右边每一项都是正数，自然大于0.

所以二楼的证明才是关键！
0404600213

引用回帖:
5楼: Originally posted by hank612 at 2016-06-07 11:25:09
你其实无意中已经说出答案了阿

如果有两个大于1，比如x,y, 那么 x 乘以 y 已经大于1。

如果恰好只有一个大于1，那么恒等式左边是一个正数减去一个负数，自然大于0

如果三个都小于1，那么恒等式右边每一 ...

我一直在考虑坐标变换或者三角代换……
Edstrayer

引用回帖:
5楼: Originally posted by hank612 at 2016-06-07 11:25:09
你其实无意中已经说出答案了阿

如果有两个大于1，比如x,y, 那么 x 乘以 y 已经大于1。

如果恰好只有一个大于1，那么恒等式左边是一个正数减去一个负数，自然大于0

如果三个都小于1，那么恒等式右边每一 ...

是的，在约束条件xy+yz+zx=1(x>0,y>0,z>0)下，不等式

[latex](1-x^2)(y-z)^2+(1-y^2)(z-x)^2+(1-z^2)(x-y)^2\geqslant 0[/latex]

与不等式：

[latex]xyz(x+y)(y+z)(z+x)\geqslant(1-x^2)(1-y^2)(1-z^2)[/latex]

相互等价，彼此可互推。
i维数

我就只会硬算。。。

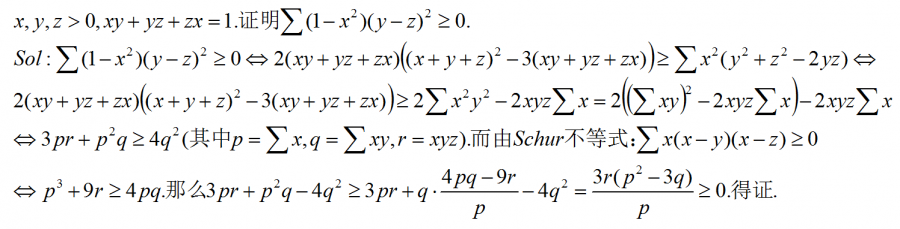
不等式.png