是不是哪里写错啦!?

引用回帖:

2楼: Originally posted by wurongjun at 2016-08-17 06:31:23
是不是哪里写错啦!?

可能你把指数的位置看错了。问题没错。

数学归纳法应该算一个。

引用回帖:

3楼: Originally posted by Mr__Right at 2016-08-17 13:04:18
可能你把指数的位置看错了。问题没错。

数学归纳法应该算一个。...

果然!so sorry!

用归纳法（暂时只会这个）验证了一下，细节就不写了，大家都会的。
问题是：右边式子第一项应该是负号？

直接计算也可以，不过计算量颇大。。。

恒等式.png

引用回帖:

6楼: Originally posted by i维数 at 2016-08-18 22:56:31
直接计算也可以，不过计算量颇大。。。

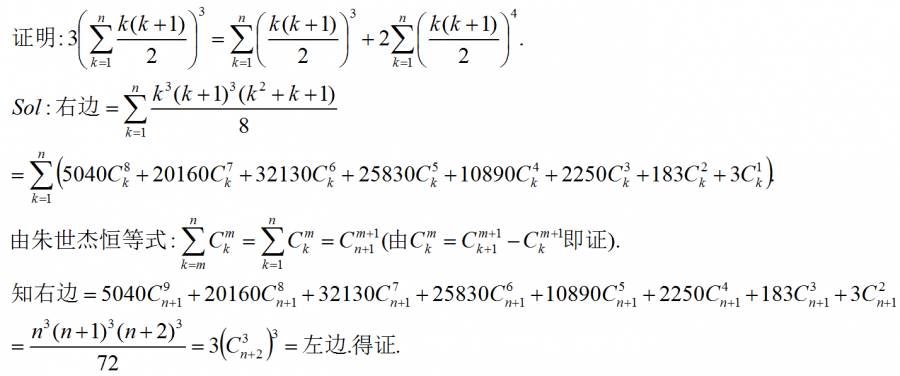
恒等式.png

@i维数 的计算功力深厚无比，大赞。

我捣鼓一个几乎不需要计算的思路，画蛇添足哈。

假设有m串糖葫芦，每串上有(n+2)个山楂， 楼主可以在每串上随便挑三颗吃，于是有
[latex]{\binom{n+2}{3}}^m[/latex]种吃法。

当然，我们可以假定在这m串中，最大的序号等于(k+2), 其中1<=k<=n. 那么会有m种子情况。

情况一，m串的最大序号都等于(k+2), 那么每串可以挑的吃法只剩下[latex]\binom{k+1}{2}[/latex]了， 于是情况一总共有[latex]{\binom{k+1}{2}}^m[/latex]种。

情况二， m串中恰好有(m-1)串的最大序号等于(k+2). 那么先挑一串最大序号小于等于(k+1)的，该串有 [latex]\binom{k+1}{3}[/latex]种吃法，剩下的每串均有[latex]\binom{k+1}{2}[/latex]。 于是情况二总共有[latex]\binom{m}{1}\cdot \binom{k+1}{3}\cdot {\binom{k+1}{2}}^{m-1}[/latex]种。

。。。
情况j, m串中恰好有(m-j+1)串的最大序号等于(k+2), 有上面分析，这种情况下有[latex]\binom{m}{j-1}\cdot {\binom{k+1}{3}}^{j-1}\cdot {\binom{k+1}{2}}^{m-j+1}[/latex]种吃法。

换句话说，有组合恒等式
[latex]{\binom{n+2}{3}}^m=\sum_{k=1}^{n}\sum_{j=0}^{m-1}\binom{m}{j}{\binom{k+1}{3}}^{j} {\binom{k+1}{2}}^{m-j}[/latex]

注意到[latex]\binom{k+1}{3}=\binom{k+1}{2}\frac{k-1}{3}[/latex], 恒等式还可以写成
[latex]{\binom{n+2}{3}}^m=\sum_{k=1}^{n}{\binom{k+1}{2}}^{m}\sum_{j=0}^{m-1}\binom{m}{j}\left(\frac{k-1}{3}\right)^{j} [/latex]

让m=1, 就有[latex]\sum_{k=1}^n \frac{n(n+1)}{2}=\binom{n+2}{3}[/latex];

让m=3, 就有[latex]{\binom{n+2}{3}}^3=\sum_{k=1}^{n}{\binom{k+1}{2}}^{3}\frac{k^2+k+1}{3} [/latex]

这经过变形， 恰好就是 @Edstrayer 版主大神  的恒等式
，

引用回帖:

7楼: Originally posted by hank612 at 2016-08-19 13:05:42
i维数 的计算功力深厚无比，大赞。

我捣鼓一个几乎不需要计算的思路，画蛇添足哈。

假设有m串糖葫芦，每串上有(n+2)个山楂， 楼主可以在每串上随便挑三颗吃，于是有
{\binom{n+2}{3}}^m种吃法。

当然， ...

真是汗颜呐。。。我的计算都是在软件的辅助下完成的。。反倒是大神你的方法真是绝妙！这构造组合模型的方法太难想到啦，大神你是怎么想到这样证明的？