一道平面几何的习题02
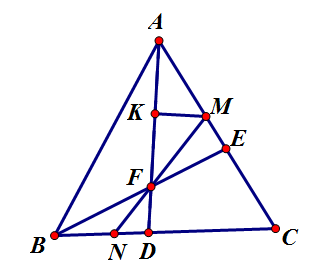
题目(XXXXX，2016)：如图所示，在正三角形ABC中，点D，E分别是边BC和CA上的动点，使得BD=CE，连接AD和BE，相交于点F，设K是AF的中点，作[latex]KM\bot AF[/latex]，且直线KM交CA于M，连接MF并延长交BC于N。
试证：（1）BN=NF
（2）设AB=a，AM=b，试计算DN的长=？
Hint：用含a，b的代数式表示DN，并指明a，b应满足的约束条件。
捕获02.png
返回小木虫查看更多
今日热帖
猜你喜欢
板块导航
- 网络生活
- 资源共享
- 化学化工
- 专业学科
- 科研生活
- 生物医药
- 材料
- 计算模拟
- 学术交流
- 出国留学
- 注册执考
24小时热帖
换一批
- 下载小木虫APP
- 与700万科研达人随时交流
-
二维码
-
IOS
-
安卓
京公网安备 11010802022153号
角MFE等于角BAF等于角FBN，所以三角形NBF等腰吧
https://muchong.com/bbs/viewthread.php?tid=9010884&fpage=1
见此贴105楼
同时希望版主提供自己的解答
233
1.jpg
，
之前发的第二问的解是用建系，过程极其死板没有参考性。不过又获得了一个不需要建系的方法。
结果正确。
[latex]DN=\frac{2ab(a-b)}{(a+b)(a+3b)}[/latex]