一道平面几何的习题02
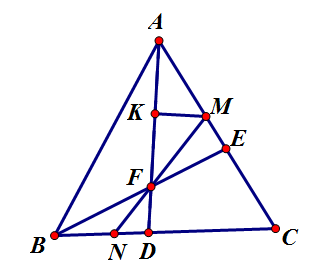
题目(XXXXX，2016)：如图所示，在正三角形ABC中，点D，E分别是边BC和CA上的动点，使得BD=CE，连接AD和BE，相交于点F，设K是AF的中点，作[latex]KM\bot AF[/latex]，且直线KM交CA于M，连接MF并延长交BC于N。
试证：（1）BN=NF
（2）设AB=a，AM=b，试计算DN的长=？
Hint：用含a，b的代数式表示DN，并指明a，b应满足的约束条件。
捕获02.png
返回小木虫查看更多
今日热帖
猜你喜欢
板块导航
- 网络生活
- 资源共享
- 化学化工
- 专业学科
- 科研生活
- 生物医药
- 材料
- 计算模拟
- 学术交流
- 出国留学
- 注册执考
24小时热帖
换一批
应助之星
- 下载小木虫APP
- 与700万科研达人随时交流
-
二维码
-
IOS
-
安卓
京公网安备 11010802022153号
[latex]CE^2+a^2-2aCE\cos\frac{\pi}{3}=AE^2+a^2-2aAE\cos\frac{\pi}{3}[/latex]
这里CE=x+y，AE=a-(x+y)，代入上式并化简得到的是0=0，解不出y来
，
先以B为原点建系，用解析几何求出BD=a(a-b)/(a+b),然后在三角形MCN中利用余弦定理求出BN=NF=a(a-b)/(a+3b),ND=BD-BN=2ab(a-b)/((a+b)(a+3b))
https://muchong.com/3g[/url] ]
真·几何法
[latex]\triangle ACG\cong\triangle ABF[/latex]
怎么推出BE=CF？
[latex]\frac{CM}{AM}=\frac{CH}{AF}[/latex]是怎么来的？
写错啦，BF=CG