Edstrayer版版这个积分说实话好难算。。。长话短说，用留数定理算貌似是一个很好的方法。或许可以计算ln(a+bcos(x)+cos(2x))这种形式的积分

简述下计算步骤：
1、利用cos(x)的偶函数和周期性，转换成0到2pi上的积分，当然要有系数1/2
2.  用欧拉公式转换,
3. 用留数定理计算，恰好有3个零点，一个是0，还有一对是方程的根。。。。
4.最后相加结果取实部即可

https://muchong.com/bbs/viewthread.php?tid=7140294

就当是炒冷饭吧， 上面帖子中提到了一个引理，利用含参数积分的性质：

当 A>1时，[latex]\int_0^{\pi}\ln(A-\cos{t})dt=\int_0^{\pi}\ln(A+\cos{t})dt=\pi\ln\frac{\sqrt{A^2-1}+A}{2}[/latex]

由此立得 @Edstrayer 版主大神 的积分公式

前两个解答在《微积分教程》第二卷中可以找到，还有一个用递推方法来解决的在里面也有，我没找到，有兴趣的话可以去看看。

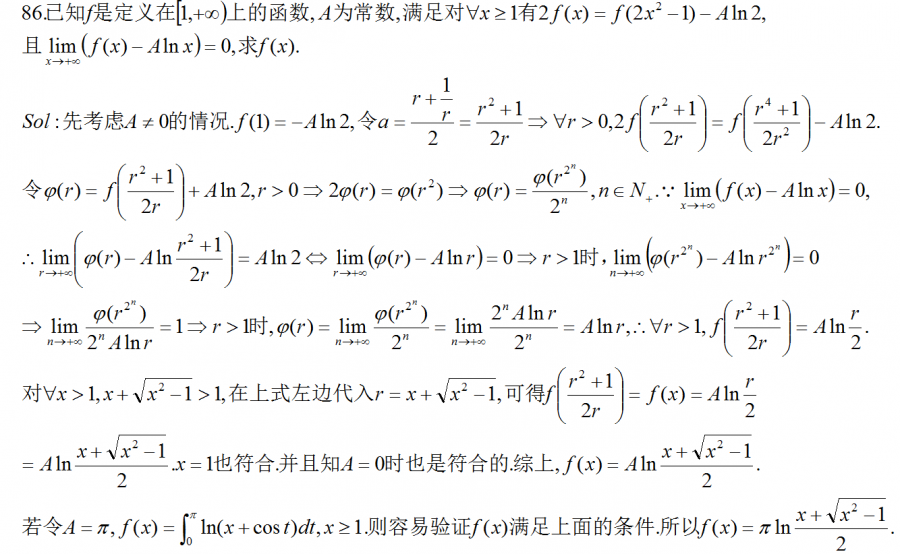
积分1.png



积分2.png



积分3.png



积分4.png



积分5.png

，