求次数最小的整系数多项式f(x)，使得[latex]\sqrt{3}+\sqrt[3]{5}[/latex]是f(x)的一个根。 返回小木虫查看更多
6次多项式： 图片1.png
代数的东西鄙人讲不出多少道理，但所求的多项式应该是把所有形如 [latex]x-(-1)^i\sqrt{3}-\omega^j\sqrt[3]{5}\quad i=0,1;\ j=0,1,2[/latex] 的一次式（共6个）乘起来的结果。
[latex]x^6-9x^4-10x^3+27x^2-90x-2[/latex]
返回小木虫查看更多
京公网安备 11010802022153号
6次多项式：
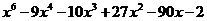
图片1.png
代数的东西鄙人讲不出多少道理，但所求的多项式应该是把所有形如
[latex]x-(-1)^i\sqrt{3}-\omega^j\sqrt[3]{5}\quad i=0,1;\ j=0,1,2[/latex]
的一次式（共6个）乘起来的结果。
忘了说[latex]\omega[/latex]是三次本原单位根
这个解答是正确的。没错。
这样乘出来的多项式不是整系数啊？
先固定 [latex]i[/latex]，让 [latex]j[/latex] 变化，乘得的两个式子应该是
[latex](x+\sqrt{3})^3-5[/latex]
[latex](x-\sqrt{3})^3-5[/latex]
这两个式子再乘就是整系数多项式了。
那这样得到的多项式就是2楼给出的：
[latex]x^6-9x^4-10x^3+27x^2-90x-2[/latex]
，