一个极限加边的计算
题目：设[latex]f(x)\in C^{2}_{[0,1]}[/latex]，试计算极限：
[latex]\lim\limits_{n\to+\infty}n\left(n\int_0^1x^nf(x)dx-f(1)\right)=?[/latex]
返回小木虫查看更多
今日热帖
板块导航
- 网络生活
- 资源共享
- 化学化工
- 专业学科
- 科研生活
- 生物医药
- 材料
- 计算模拟
- 学术交流
- 出国留学
- 注册执考
24小时热帖
换一批
- 下载小木虫APP
- 与700万科研达人随时交流
-
二维码
-
IOS
-
安卓
京公网安备 11010802022153号
-f(1)-f'(1).
首先，极限中的积分的下端点可以换成任意固定的数A，其中0<A<1，因为f有界。
然后，挑选A和C,使得|f(x)-f(1)+f'(1)(x-1)|<C(x-1)^2对任意A<x<1.
最后，计算即可（容我偷个懒，不贴太繁琐）。
用分部会很方便。
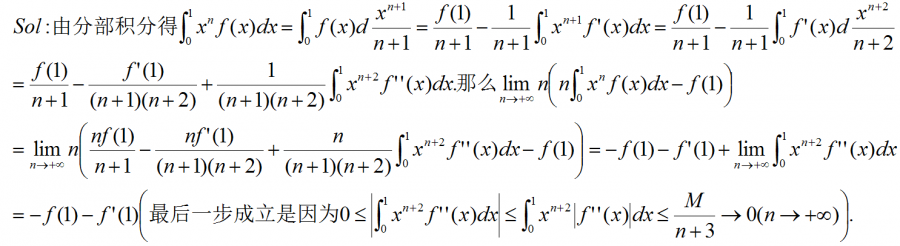
极限加边.png
这个证明有两处凝问:1.最后第二步中第一项-f(1)是怎么得到的呢?
2.最后的结果中,最后的积分余项中,函数的二次导数怎么就是有界M呢
，