一个无穷级数的求和?
试求出下面的无穷级数的和:
\sum_{n=1}^{+\infty}(-1)^{\frac{1}{2}n(n+1)}\frac{1}{2n-1}=?
[latex]\sum\limits_{n=1}^{+\infty}(-1)^{\frac{1}{2}n(n+1)}\frac{1}{2n-1}=?[/latex]
[ Last edited by Edstrayer on 2014-4-29 at 17:41 ]
今日热帖
试求出下面的无穷级数的和:
\sum_{n=1}^{+\infty}(-1)^{\frac{1}{2}n(n+1)}\frac{1}{2n-1}=?
[latex]\sum\limits_{n=1}^{+\infty}(-1)^{\frac{1}{2}n(n+1)}\frac{1}{2n-1}=?[/latex]



是下面的级数求和?
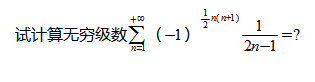
无穷级数的求和001.png
-1.11067073453997 用软件算吧...
原式=(1-1/3)+(1/5-1/7)+(1/9-1/11)+(1/13-1/15)+......
=1-(1/3-1/5)-(1/7-1/9)-(1/11-1/13)-......
若各取前3项计算,则得:
2578/3465<原式<847/945
用软件算的那是计算数学,得到的是近似值;用逻辑推导的精确解析式那是基础数学,得到的是精确值,两者的思想、方法,工具与技巧相差很远的。……
计算是错的,首项就搞错了符号
该级数=-1-1/3+1/5+1/7-1/9-1/11+1/13+1/15-……
根据楼主的提示,
Emuch001.jpg
,
这里的方法是正确的,但是计算结果不对,……
级数的正确和是-\frac{\sqrt{2}\pi}{4}
楼主英明.
让 A=arctan(1- Sqrt[2]), B=arctan(1+Sqrt[2]), 那么 tan(A-B)= (tanA-tanB)/(1+tanA*tanB)= -Infinity.
因此 A-B= -Pi/2, 从而 f(1)= ( -Pi/2 )/ Sqrt[2]= -Sqrt[2]*Pi/4.
一个简单的答案被一个很吓人的表达式搞砸了...