https://dlmf.nist.gov/25.11
有现成答案

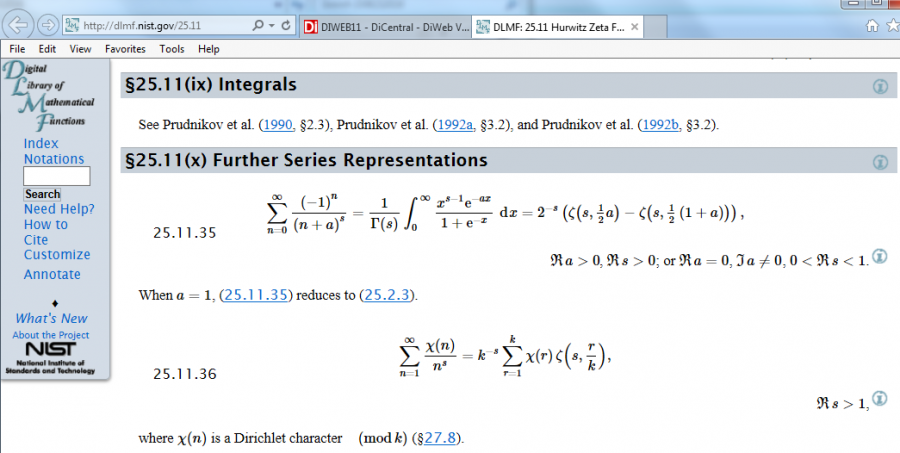
要利用到的公式: 首先(25.11.35), 其次 (25.11.16), 最后 (25.11.14)

Emuch024 Hurwitz 2.png



Emuch024 Hurwitz.png

几时能把-1变成1，才牛！

我只是来膜拜一下hank大神和版主大神

[latex]\sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)^{2m+1}} =\frac{(-1)^{m-1} 2^{2m} \pi^{2m+1}}{(2m+1)!}\sum_{n=0}^{2m+1}\sum_{k=0}^n \frac{(-1)^k C_n^k}{n+1}(k+\frac{1}{4})^{2m+1}[/latex]（从2楼推导）

CODE:

clc;clear;
format rat;
for m=1:3
        p(m)=(-1)^(m-1)*2^(2*m)/(2*m+1);s=0;
        for n=0:2*m+1
                for k=0:n
                        s=s+(-1)^k*nchoosek(n,k)*(k+1/4)^(2*m+1)/(n+1);
        end
    end
    p(m)=s*p(m);
end
p

p =

       1/16           5/64          61/256   

[latex]\sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)^3}=\frac{\pi^3}{16\times 2!}[/latex]
[latex]\sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)^5}=\frac{5\pi^5}{64\times 4!}[/latex]
[latex]\sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)^7}=\frac{61\pi^7}{256\times 6!}[/latex]
，

https://muchong.com/bbs/viewthread.php?tid=10270516&page=1

10楼的

[latex]\sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)^{2m+1}}=\frac{(-1)^m E_{2m}\pi^{2m+1}}{4^{m+1}(2m)!}[/latex]

CODE:

clc;clear;
format rat;
for m=1:3
        p(m)=i*(-1)^m/4^(m+1);s=0;
        for k=1:2*m+1
                for j=0:k
                        s=s+(-1)^j*nchoosek(k,j)*(k-2*j)^(2*m+1)/(2^k*i^k*k);
        end
    end
    p(m)=s*p(m);
end
p

p =

       1/16           5/64          61/256

符号没有问题