小木虫

当前位置：首页 > 有奖问答 >数学大神啊，救救我吧，求函数的表达式，能举个例子就行了。

数学大神啊，救救我吧，求函数的表达式，能举个例子就行了。

作者 taianxt: 来源: 小木虫 450 9 举报帖子

已知：
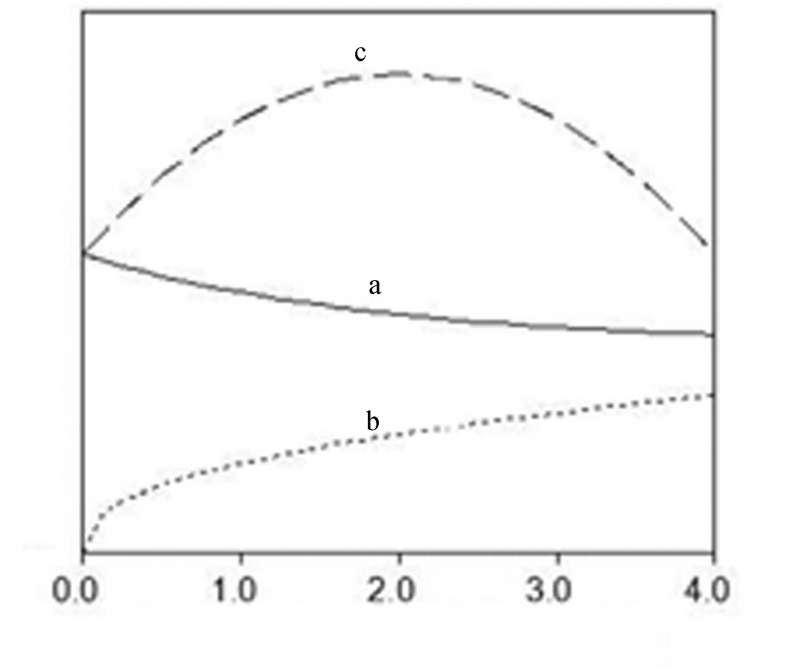
函数a：在区间内是单调减函数，只是减少的幅度逐渐变小，具体函数表达式不知道；
函数b：在区间内是单调增函数，增加的幅度不知道，具体函数表达式不知道；
函数c：在区间内是先增后减，最大值在区间的中点附近，是函数a和函数c的和，即c=a+b；
求解
函数a，b，c的表达式，各举个例子就行了，要满足以上3个条件。

1.jpg 返回小木虫查看更多

今日热帖

精华评论

Edstrayer

[latex]a(x)=-x(x\in[0,4])[/latex]

a(x)单调递减，变化速度随着x增大而逐渐变小

[latex]b(x)=-e^{2-x}(x\in[0,4])[/latex]

b(x)单调递增，

[latex]c(x)=a(x)+b(x)=-x-e^{2-x}(x\in[0,4])[/latex]

则c(x)在[0,2]上是增函数，在[2,4]上是减函数，最大值在x=2处取得。
如上构造的三个函数a(x)，b(x)，c(x)满足楼主的三个要求。
taianxt

引用回帖:
9楼: Originally posted by Edstrayer at 2015-01-29 04:39:21
a(x)=-x(x\in)
a(x)单调递减，变化速度随着x增大而逐渐变小
b(x)=-e^{2-x}(x\in)
b(x)单调递增，
c(x)=a(x)+b(x)=-x-e^{2-x}(x\in)
则c(x)在上是增函数，在上是减函数，最大值在x=2处取得。
如上构造的三个函 ...

虽然答案不太合适，但对我启发很大，谢谢。满分
，