origin 里 “三次样条函数拟合” 与“三次多项式拟合”是一回事吗？如图
请origin高手帮忙解答一下：
1.一个公式是用：Mathematics-Interpolate/Extrapolate-Cubic Spline
2. 另一个是：Polynomial fitting-polynomial Order (改成3)
这两个公式理论上有什么区别，用哪一个更为准确些
如图： 原始数据：
X Y
-6.90776 79.6
-4.60517 107.3
-2.30259 123.2
0 149.1
2.30259 159
2.99573 170.1
3.91202 177.2
用公式1得到的拟合图为：
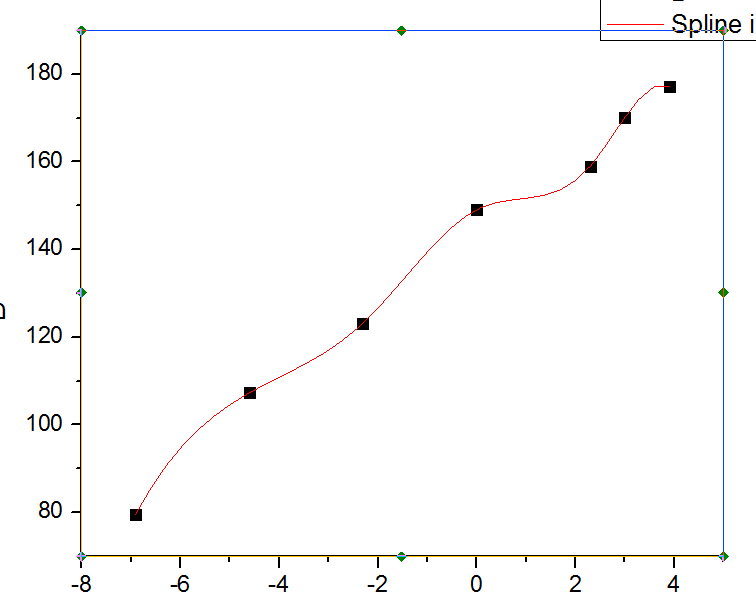
用公式2得到的拟合图为：
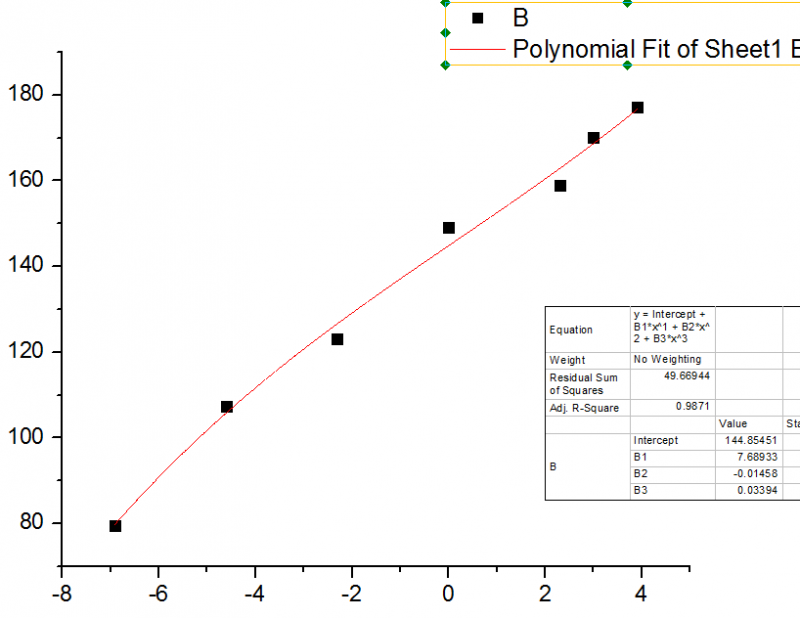
返回小木虫查看更多
今日热帖
京公网安备 11010802022153号
第一种方法确切的说是 三次样条插值；
第二种方法是三次多项式拟合，可以得到具体的拟合曲线方程。
插值法得到的曲线，数据点都落在插值曲线上，但是实际试验数据存在一定的离散性，如果是总结趋势性的规律我个人觉得第二种方法就可以了。
嗯，很有道理，谢谢
也就是说，第一种方法中 每两个数据点之间都是用的三次多项式拟合，即分段的三次多项式拟合。 而第二种方法中 整体数据用了只一次三次多项式拟合
，