为什么利用MATLAB拟合得到的多项式函数R=0.9992,而求出来的Z值与实际Z值误差却很大?
以下是MATLAB拟合结果:
Linear model Poly55:
f(x,y) = p00 + p10*x + p01*y + p20*x^2 + p11*x*y + p02*y^2 + p30*x^3 + p21*x^2*y
+ p12*x*y^2 + p03*y^3 + p40*x^4 + p31*x^3*y + p22*x^2*y^2
+ p13*x*y^3 + p04*y^4 + p50*x^5 + p41*x^4*y + p32*x^3*y^2
+ p23*x^2*y^3 + p14*x*y^4 + p05*y^5
Coefficients (with 95% confidence bounds):
p00 = 0.0226 (-0.06975, 0.115)
p10 = 0.2718 (0.06219, 0.4814)
p01 = -0.6836 (-3.116, 1.748)
p20 = 9.223 (8.684, 9.762)
p11 = -6.219 (-10.63, -1.808)
p02 = 8.048 (-17.54, 33.64)
p30 = -7.992 (-9.399, -6.586)
p21 = -154.4 (-162.9, -146)
p12 = 53.07 (18.3, 87.84)
p03 = -46.51 (-181, 87.95)
p40 = -264.8 (-268.5, -261)
p31 = 92.77 (78.05, 107.5)
p22 = 845.7 (801.2, 890.2)
p13 = -199.8 (-321.4, -78.15)
p04 = 132.5 (-220.4, 485.3)
p50 = 16.18 (5.436, 26.93)
p41 = 1226 (1207, 1246)
p32 = -260.5 (-298.9, -222.1)
p23 = -1520 (-1598, -1442)
p14 = 279.7 (120.4, 438.9)
p05 = -149.1 (-519, 220.9)
Goodness of fit:
SSE: 4.894e-09
R-square: 0.9992
Adjusted R-square: 0.9992
RMSE: 1.347e-06
但是通过excel里的数据发现,误差大都很大,甚至达到200%,有大神解答一下吗,或者有没有更好的方案?谢谢各位@月只蓝




 京公网安备 11010802022153号
京公网安备 11010802022153号
用nlinfit函数,可以得到如下系数
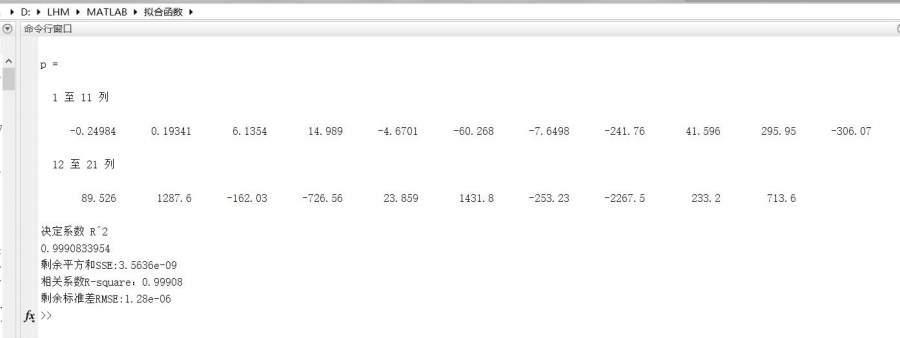
p 0=-0.24984 ;p 1= 0.19341 ;p 2= 6.1354 ;p 3= 14.989 ;p 4= -4.6701
p 5= -60.268 ;p 6= -7.6498 ;p 7= -241.76 ;p 8= 41.596 ;p 9= 295.95
p 10= -306.07 ;p11=89.526 ;p 12= 1287.6 ;p 13 = -162.03 ;p 14= -726.56
p 15= 23.859 ;p 16= 1431.8 ;p 17= -253.23 ;p 18= -2267.5 ;p 19= 233.2;p 20 = 713.6
其模型为
y=p0+ k1*x + p2*y +p3*x.^2 + p4*x.*y + k5*y.^2 + p6*x.^3 + p7*x^2.*y + p8*x.*y.^2 + p9*y.^3
+p10*x.^4 + p11*x.^3.*y +p12*.^2.*y.^2+ p13*x.*y.^3 +p14*y.^4 + p15*x.^5 +p16*x.^4.*y +p17*x.^3.*y.^2 + p18*x.^2.*y.^3 + p19*x.*y.^4 + p20*y.^5
123.jpg
次数太多了,缺乏一定的数学意义了
不要用显示出来的数据(拟合参数值)
save 到工作空间。你的是5次方,可能对精度要求高点。
代入下面精度高的参数值,结果很好的
p00 = 0.0226044691022134
p10 = 0.271779887157913
p01 = -0.683619253452661
p20 = 9.22296034668144
p11 = -6.21944914640458
p02 = 8.04796072285362
p30 = -7.9923682787726
p21 = -154.444571814872
p12 = 53.0716540530778
p03 = -46.5141174297546
p40 = -264.756721494465
p31 = 92.768794351253
p22 = 845.695876099824
p13 = -199.764467820342
p04 = 132.492480426455
p50 = 16.1821775676906
p41 = 1226.2449723814
p32 = -260.475968318764
p23 = -1520.07977352788
p14 = 279.668886213386
p05 = -149.0617545096
R: 0.999620739860511
R^2: 0.999241623559275
RMSE: 1.34215868564752E-6
SSR: 4.89437646007633E-9,