概率统计上的一个计算问题，真心搞糊涂了，重金求助！
如题，请高手不吝赐教，问题描述见图片：
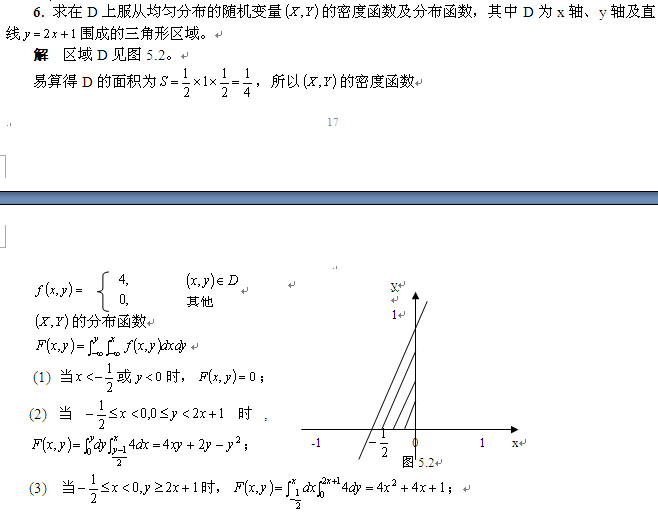
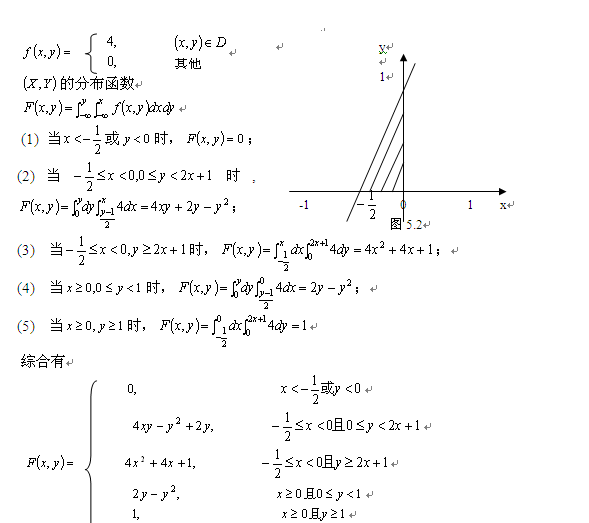
因为二重积分通常要化为二次积分进行计算，这就涉及到先对哪个变量积分的问题，按道理说先对哪个变量积分都不要紧的，只要积分上下限设置正确结果应该是一致的，可是我对其中的（2）和（4）操作的时候怎么都搞不定，比如（4）答案中是先对x后对y积分，我想先对先对y后对x积分，反复尝试却不能算出一致的结果（甚至不清楚如何设置积分域了），（2）也存在这样的问题，请高手给予指点，先表示感谢！
二次积分1.png
二次积分2.png
返回小木虫查看更多
今日热帖
京公网安备 11010802022153号
你的"综合有"答案是完全正确的, 由于不论(x,y)在哪里出现, 它的左下方交D最复杂也不过是梯形, 所以用梯形面积公式最快了.
不过楼主感到困惑的是积分区域和积分次序.我觉得你的问题是把常量(x,y)与积分变量(s,t)混为一谈,自己把自己绕进去了.
比如说区域(2): 当点(x,y)满足 -1/2<x<0, 0<y<2x+1时, 被积二元函数是f(s,t)=4 常数函数, 积分区域是: (t-1)/2 < s <x, 0<t<y. (画图可知)
于是[latex]F(x,y)=\int_{0}^{y}dt \int_{(t-1)/2}^{x} 4 ds=4(xt+\frac{t}{2}-\frac{t^2}{4}|_{0}^{y}=4xy+2y-y^2[/latex] 非常吻合.
我想把积分变量置为（x,y)抑或(s,t)并不重要，我主要关心的问题是交换积分次序后结果应该是一致的，比如（5）：但是我无法对（2）和（4）实现这样的操作。问题也就出在这里。还望进一步指点，谢谢！
（5）如下：
交换次序.png
，
积分交换次序 牵涉到如何表示积分区域.
以(2)为例, 该梯形按照先ds(x轴方向)后dt(y轴方向)表示是:
(t-1)/2 < s < x, 0<t<y
同样梯形按照先dt(y轴方向)后ds(x轴方向)表示则是
-1/2 < s <x, 0 <t < min(2s+1, y)
楼主可以自己证明: [latex]\int_{0}^{y} dt \int_{(t-1)/2}^{x} ds =\int_{-1/2}^{x}ds \int_{0}^{\min(2s+1,y)} dt[/latex]
，问题来了，我该如何把其余的金币返给你呢