已知一约束条件,求解另一个积分。。!!!!!
图中已知第一个方程,如何求解下面一个积分?
麻烦给出求解过程(代码)
C0为未知常数,ρ为任意正数
一种方法是先给出ρ的值,最后将结果除以ρ^2,但是感觉这种这种方法不太严谨,寻求其他方法求得积分后关于ρ的表达式
最后积分后的结果应该是 0.158ρ^2
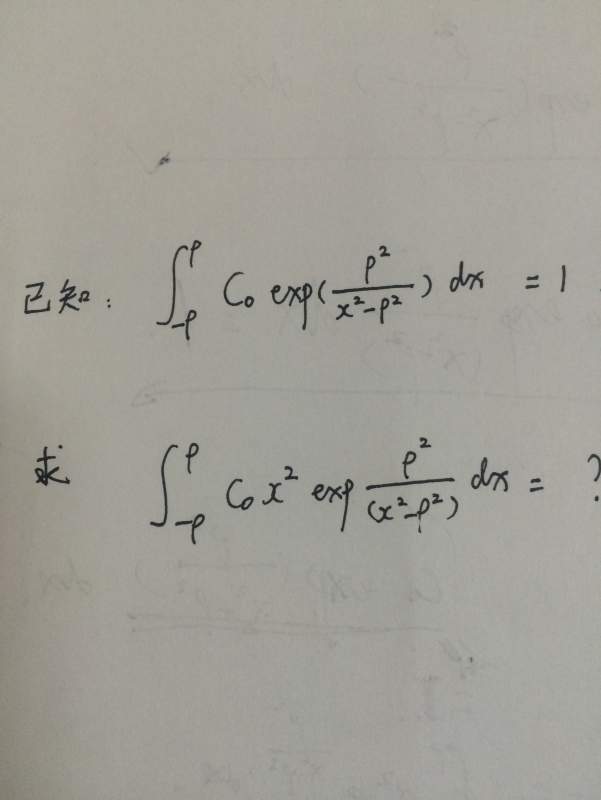
IMG_0982.JPG![]() 返回小木虫查看更多
返回小木虫查看更多
今日热帖
图中已知第一个方程,如何求解下面一个积分?
麻烦给出求解过程(代码)
C0为未知常数,ρ为任意正数
一种方法是先给出ρ的值,最后将结果除以ρ^2,但是感觉这种这种方法不太严谨,寻求其他方法求得积分后关于ρ的表达式
最后积分后的结果应该是 0.158ρ^2
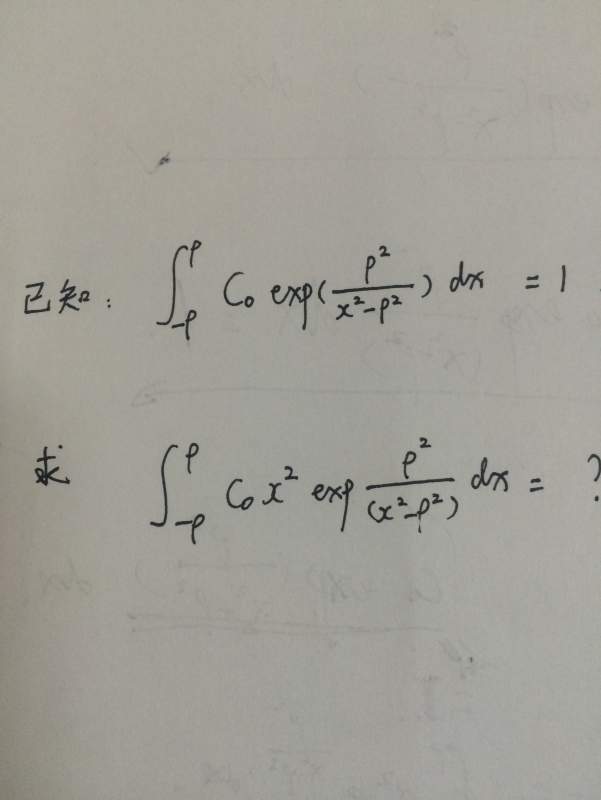
IMG_0982.JPG![]() 返回小木虫查看更多
返回小木虫查看更多



这应该是一个无法用简单初等函数表达的超越数。
不是也许,应该是肯定。
注意上面一个定积分为1,下面式子除以上面的就可以把C0约掉,所以C0只是干扰项,没有意义。
对分子和分母的两个积分可以作变量代换,把 x 用 ρ*t 替换掉,则定积分上下限为(-1,1),被积函数中可以不显含除t以外的其它变量,从而两个定积分是常量。它们有一个系数恰好是ρ^2
关键在于这两个定积分,应该都是特殊函数、无法用根式形式或其它简单形式表达;但是可以求它们的数值解到任意精度。——问题也只能解到这个程度了。
测试下公式
[latex]{\int_{-1}^1 t^2 e^\tfrac{1}{t^2-1}dt}\left({\int_{-1}^1 e^\tfrac{1}{t^2-1}dt}\right)^{-1}=[/latex]
,
公式自己推吧。这里的LaTeX输入方式太不友好了。