求取多解的非线性代数方程所有数值解的方法

作者 月只蓝: 来源: 小木虫 400 8 举报帖子

0. 引言
一些非线性方程在实数范围内存在多解，本帖要讨论的正是求得所有的这些解的方法。多解方程，其解的个数不同，求解难度也不同，本帖将针对解个数较少和解个数较多的两种情况，各举一例进行讨论，并提出相应的方法和代码，作者希望本帖提出的方法和代码能具有较强的普适性。
本帖所采用软件及其版本：
（1）1stOpt 1.5
（2）MATLAB 2010a
（3）Maple 18

1. 解个数较少的情况
例：求出如附图1所示方程的全部解（方程出处：https://muchong.com/bbs/viewthread.php?tid=9911763&fpage=1）。

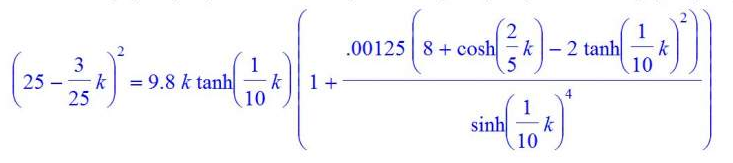
附图1.png
具体步骤如下：

步骤1：画出方程图形，直观上确定解的个数
为了画出方程图形，首先须正确输入该方程，如果输入的原始方程都是错误的，就更不用谈结果的正确性。
因此，在步骤1中还包括一个方程输入预检验的步骤。

步骤1.1：方程输入预检验
根据附图1，可将原始方程写为：
y=(25-(3/25)*k)^2-9.8*k*tanh((1/10)*k)*(1+(0.125e-2*(8+cosh(.4*k)-2*tanh(.1*k)^2))/sinh(.1*k)^4)
由于待求解方程形式较为复杂，须检查方程的输入是否正确。这里用到的软件是Maple，利用该软件强大的二维显示功能，可判断方程输入的正误。
将上述方程在Maple中的显示结果如附图2所示。

附图2.png
仔细比对可知，原方程输入无误。

步骤1.2：方程图形绘制
绘制原方程的图形曲线时，横轴坐标的范围尽量大一些；同时绘制出直线y=0，该直线与原方程曲线的交点，即为方程的解。
对于本例，MATLAB代码如下：

CODE:

clear all;clc

n=5000;   

k=linspace(-1000,5000,n);

y=(25-(3/25)*k).^2-9.8*k.*tanh((1/10)*k).*(1+(0.125e-2*(8+cosh(.4*k)-2*tanh(.1*k).^2))./sinh(.1*k).^4);

figure

plot(k,y,'b',[min(k) max(k)],[0 0],'r'),axis([min(k) max(k) min(y) max(y)]);

上述代码中，n表示绘图时散点的个数，n应当取为较大的数值，以防止漏解。
上述代码结果如附图3所示。从附图3中可见，原方程在k<100，以及k=1000附近存在两个解；此外，仔细观察可见，在k=0左右的细微局部也存在解，将此局部放大如附图4，可见在这细微局部内，存在两个解。

附图3.png

附图4.png

步骤2：求解
对于这种方程，MATLAB的fsolve函数可高效求解，根据步骤1.2中的分析，初值选为-0.1，0.1，100和1000，具体代码如下：

CODE:

format long

[x fval]=fsolve(@(k) (25-(3/25)*k).^2-9.8*k.*tanh((1/10)*k).*(1+(0.125e-2*(8+cosh(.4*k)-2*tanh(.1*k).^2))./sinh(.1*k).^4),[-0.1,0.1,100,1000]  )

计算结果：

CODE:

x =

  1.0e+003 *

  -0.000419092354465   0.000420785261224   0.040837844386158   1.063205199210630

fval =

  1.0e-010 *

  -0.001136868377216  -0.001136868377216   0.388240550819319   0.272848410531878

至此，用MATLAB求得了原方程全部4个解。

当然，上述求解过程也可用1stOpt实现，根据步骤1.2中的分析，通过限定未知数k取值范围的办法，可同样求解4个解，具体的代码有4段，分别如下：
限定k小于0：

CODE:

Parameters k[,0];

Function (25-(3/25)*k)^2-9.8*k*tanh((1/10)*k)*(1+(0.125e-2*(8+cosh(.4*k)-2*tanh(.1*k)^2))/sinh(.1*k)^4);

计算结果：

CODE:

目标函数值: 1.13686837721616E-13

k: -0.419092354476606

限定k在[0，1]：

CODE:

Parameters k[0,1];

Function (25-(3/25)*k)^2-9.8*k*tanh((1/10)*k)*(1+(0.125e-2*(8+cosh(.4*k)-2*tanh(.1*k)^2))/sinh(.1*k)^4);

计算结果：

CODE:

目标函数值: 1.13686837721616E-13

k: 0.420785261224372

限定k在[10，100]：

CODE:

Parameters k[10,100];

Function (25-(3/25)*k)^2-9.8*k*tanh((1/10)*k)*(1+(0.125e-2*(8+cosh(.4*k)-2*tanh(.1*k)^2))/sinh(.1*k)^4);

计算结果：

CODE:

目标函数值: 0

k: 40.8378443861602

限定k>500：

CODE:

Parameters k[500,];

Function (25-(3/25)*k)^2-9.8*k*tanh((1/10)*k)*(1+(0.125e-2*(8+cosh(.4*k)-2*tanh(.1*k)^2))/sinh(.1*k)^4);

计算结果：

CODE:

目标函数值: 1.81898940354586E-12

k: 1063.20519918986

2. 解个数较多的情况
对于解个数较多的情况，采用上述人工选取初值点的办法将比较低效而且容易漏解，举例如下：
求方程：y=sin(10*x)-log10(x) 的全部解（方程出处：https://muchong.com/bbs/viewthread.php?tid=9425648&fpage=1）。
由于原方程形式很简单，无需进一步检查方程输入的正误，采用MATLAB可绘制该方程在[0，100]范围内的图形（由于方程中对数的存在，x<0时，不存在实数解，故x<0的情况毋须考虑），代码如下，结果如附图5所示。

CODE:

clear all;clc

n=5000;

x=linspace(0,100,n);

y=sin(10*x)-log10(x);

figure

plot(x,y,'b',[min(x) max(x)],[0 0],'r');

附图5.png
由附图5可见，尽管原方程的曲线在纵轴方向剧烈震荡，但在[0，10]之外的范围不存在解，因此可进一步绘制[0，10]范围内的图形，如附图6所示。

附图6.png
可看到，该方程解的个数极多，采用上述人工选取初值点的方法就难以实施了。对于这种情况，作者的思路是这样的：从图形上至少能观察到这些解大概的取值范围，在这取值范围之内广“撒网”，取足够多的初值，求出来的结果就能遍历全部解。当然由于选取初值的个数大于解的个数，求出来的结果中肯定会有重复的，在代码中加一段去重的函数，即可将所有解求出来，具体的MATLAB代码如下：

CODE:

clear all;clc

x=fsolve(@(x) sin(10*x)-log10(x),linspace(0.2,9.7,100));

x=round(1e6*x)/1e6;

x_answer=unique(x)

计算结果：

CODE:

x_answer =

  Columns 1 through 13

    0.3601    0.6064    0.9449    1.2669    1.5516    1.9135    2.1649    2.5552    2.7814    3.1945    3.3997    3.8322    4.0192

  Columns 14 through 26

    4.4690    4.6394    5.1052    5.2602    5.7410    5.8812    6.3767    6.5024    7.0123    7.1236    7.6482    7.7445    8.2845

  Columns 27 through 31

    8.3649    8.9219    8.9842    9.5621    9.6007

至此，求得了原方程全部的31个解（如果有兴趣数一下附图6中红线和蓝线交点的个数，会发现交点个数正是31）。

[ Last edited by 月只蓝 on 2018-8-17 at 21:23 ]

今日热帖