遇到一个平面几何的证明题，不知道怎么证明，题目如下。 返回小木虫查看更多
证明：从I、J分别向GB、OC作垂线，由已知可得垂线段IP=QJ 又由于OI=OJ, 所以直角三角形OPI与OQJ全等 所以求证的两个角相等 2.JPG
应该是从I向OD作垂线 不好意思一时激动打错了
设圆与AG相较于点K，连接KO，可得三角形ＣＫＯ与三角形ＣＪＯ全等，三角形CKO全等于三角形IGO，则角ＫＯＣ＝角COJ，角KOC=角GOB，又因为AEGH和GHBF对称且全等，可角GOC=角GOD，所以角DOI=角COJ。
返回小木虫查看更多
京公网安备 11010802022153号
证明：从I、J分别向GB、OC作垂线，由已知可得垂线段IP=QJ
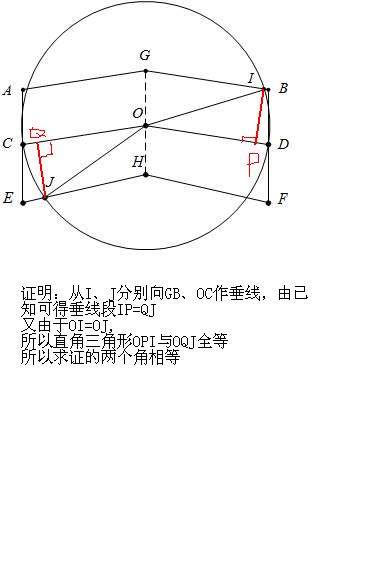
又由于OI=OJ,
所以直角三角形OPI与OQJ全等
所以求证的两个角相等
2.JPG
应该是从I向OD作垂线 不好意思一时激动打错了
设圆与AG相较于点K，连接KO，可得三角形ＣＫＯ与三角形ＣＪＯ全等，三角形CKO全等于三角形IGO，则角ＫＯＣ＝角COJ，角KOC=角GOB，又因为AEGH和GHBF对称且全等，可角GOC=角GOD，所以角DOI=角COJ。
三角形OPI与OQJ全等
这个没搞明白，为什么全等呢？
三角形ＣＫＯ与三角形ＣＪＯ全等
这个没搞明白，为什么全等呢？
IP=JQ，根据的是对称性以及平行四边形中位线到两边距离相等；
OI=OJ，同是圆的半径；
又因为是直角三角形，斜边与一条直角边分别对应相等，故两直角三角形全等（HL定理）。
所以……
，