从He2等的量子化学图形解读范德华作用(续)

Zhou2009

本帖是上帖“从He2等的量子化学图形解读范德华作用” 的续篇。所引文献也见上帖。（https://muchong.com/bbs/viewthread.php?tid=4123962&fpage=1）
也用Gaussian09计算，用Multiwfn 2.3（含Gsgrid）进行数据处理，用Gaussview、Sigmaplot作图。当距离数值不标出单位时是Å，电荷和能量数值不标出单位时是 a.u.。

一、用CCSD/aug-cc-pVTz计算并作图：
1、        算He-Ar：
取文献[3]平衡键长进行计算：3.494。
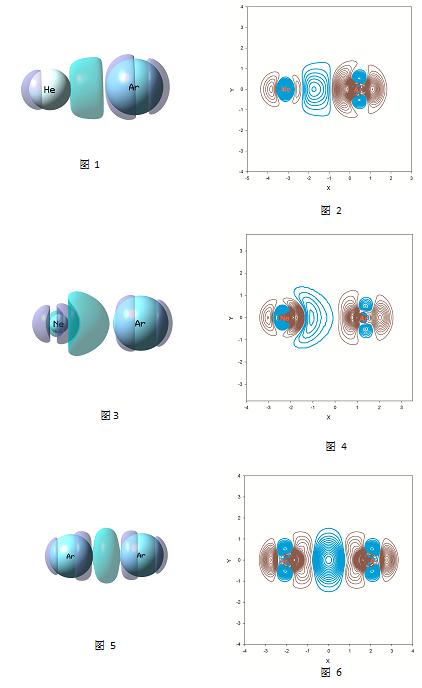
作He-Ar与自由He、Ar的Natural Orbital密度差Δρ，照例在Gaussview中观察Δρ图的容貌，见图1。等值面值取±2e^-6。紫色为正，增加电荷量为0.0005366；青兰色为负，减少电荷量为0.0005352。
进一步作截面等值线图，即图2，等值线起始值取±2e^-6。赭红为正，是电子密度增加区域；青兰色为负，是电子密度减少区域（下同）。
2、        算Ne-Ar：
取文献[3]平衡键长进行计算：3.495。
作Ne-Ar与自由Ne、Ar的Natural Orbital密度差Δρ，照例在Gaussview中观察Δρ图的容貌，见图3。等值面值取±5e^-6。紫色为正，增加电荷量为0.001114；青兰色为负，减少电荷量为0.001118。进一步作截面等值线图，即图4，等值线起始值取±5e^-6。
3、算Ar2：
取文献[3]平衡键长进行计算：3.779。
作Ar2与两个自由Ar的Natural Orbital密度差Δρ，照例在Gaussview中观察Δρ图的容貌，见图5。等值面值取±5e^-6。紫色为正，增加电荷量为0.001922；青兰色为负，减少电荷量为0.001923。进一步作截面等值线图，即图6，等值线起始值取±5e^-6。

上面He-Ar、Ne-Ar和Ar2的Δρ图景，与前帖He2、Ne2、He-Ne的Δρ图景大体上如出一辙，总的图景是一致的。

从各Δρ图看来，当两个电子云球相遇、相撞，由于双方成对电子的强大的Pauli互斥，二核中间的电子明显减少了，电子云球变形了，电子转移到二核的背面去了；同时还看到，二核之间形成了饼状、球状、哑铃状的密度增加区域，这是共享电子在大幅度增加（当然是相对于当前的数量级而言）。

可以看到，为了解决电子相关，极其高深的量子化学理论模型、方法，极其复杂的基组、数学运算，得到的却是极其简单明了的电子密度变形的图景！在成千上万密度差精确数据所作的图形基础上，展现了新的简单的质，从自由原子到准分子发生的变形密度（deformation density），被密度差Δρ如实地作了写照。

（此外，在Δρ图，除了在Ne 或者Ar的背后看到密度增加之外，如果将等值面或等值线的起始绝对值进一步取小，还会看到月芽形的密度减少。这是由于作的是全电子密度差，当Ne或者Ar图取Px-Px成键时，必然也包含Ne或者Ar的Py和Pz，它们也正在Ne或者Ar的背后，由于Ne或者Ar背后密度的增加、对核的屏蔽会增加，核对Py和Pz的吸引会减弱，从而使Py和Pz有点膨胀、密度有所降低，呈月芽形的密度减少，成键前后的Py和Pz微有变化，并没有完全被抵消。）

二、范德华作力形成的过程及本质的再叙述：
以耦合簇为代表的多种量子化学方法，精确地考虑、计算了电子相关，不仅采用大型的基组，尽可能宽广地、精细地提供电子密度变形所需要的基函数空间（足够的极化和足够的弥散），而且更进一步开放了所有的轨道能级，使变形的电子可以在更高的轨道以小分数占据，给电子密度变形以更高的能级空间，以充分表达电子相关引起的电子密度形变。
这样一来，耦合簇等方法不仅精确地计算出了原子之间形成范德华作用的距离和能量，而且合理地、定量地给出了范德华作用引起的电子密度变形。
然而这密度变形常常不被人注意，主要原因是以前许多方法不能象耦合簇等如此精确地考虑、计算电子相关，以前给出的密度变形并不准确、并不合理。
其实密度变形比健长、能量更能揭示范德华作用的秘密！

这些图景清晰地表明：当两个电子云球相遇、相撞，由于双方成对电子的强大的Pauli互斥，二核正面相对之处电子相对减少了，回避、转移到二核的背面了。同时，这二核之间的电子适当减少，既减小了双方电子的强大的Pauli互斥，又使二核相对的正面出现一定程度的裸露，吸引电子能力有所增强，使二核之间电子呈现饼状、球状、哑铃状地增加，形成一种共享电子增加的图景。这共享电子在二核中间的增加，又削弱了二核之间的斥力。形成一个在适当的距离，中间电子被适当挤走，双方共享电子适当增加，以至有足够的共享电子吸引力来平衡电子之间的排斥、核之间的排斥，维系着体系，达到排斥与吸引的平衡，形成了有固定键长、固定结合能的所谓范德华力。
由此可以看到，范德华作用也是双方波函数在起作用，构造了一个双方原子核共享电子的图景，与共价的概念同出一辙，只是大小相差一两个数量级而已。文献对惰性气体二体准分子随原子间距变化作的基态势能曲线，与通常的共价健基态势能曲线在形态上也是完全一致的。

并不是自然而然就总有那么一个范德华力在那里，范德华力是电子云球相碰时发生形变而产生的，是双方波函数在起作用，是“无中生有”！

范德华力的本质仍然是一种特殊的共享电子，共享电子的范德华力是一种化学力。

三、范德华力真还是电子的“瞬间运动出现的瞬间偶极矩间的作用”吗？
然而对He-He等这样的范德华作用，多少年来一直理解为“电子的瞬间运动出现的瞬间偶极矩之间的作用”。
其实瞬间偶极矩间作用的模型猜想看起来简单，但潮动着的这种瞬间偶极如何维持一个准确固定的健长、准确固定的结合能，并不能进一步具体作计算、处理。这种瞬间偶极是不稳定的体系，会立即回复到原位，对惰性双原子来说更是随合随分，不可能定格停留在单边倾倒的瞬间偶极。这种一边倒的瞬间偶极，虽然会增加一点静电相互作用，但是这种一边倒的电子离心不与核重合必然会使能量更加升高，二核会立即把它们拉回来、回归基态。何况两个惰性原子因瞬间偶极-偶极作用而在一起了，它们有一致方向的偶极，为什么不导致第三、第四一直连下去？

当然，从上面耦合簇方法反映的密度差各个图景来看，偶极还真是都发生了！从每一个原子来细看，它在前面、后面都增加了电子，核中间电子却减少了，两极化了。
这时如果单从左边的原子看过去，它向中间增加了电子，产生偶极，作为回应，右边的原子也在同一方向—背面增加了电子，也形成所谓偶极，构成了偶极-偶极作用。但这种偶极不是单向的，而是双向的，从右边的原子看过去，也存在这种偶极-偶极作用。只有这种双向的偶极才可以是稳定存在的。这不过是从另一种视角、从一个侧面来看而已。

传统、经典的“瞬间偶极-偶极作用”的模型猜想，认为范德华作用纯粹是静电的偶极-偶极起作用，然而耦合簇等方法全面、精确地计算，证明了范德华作用还是一种双方波函数在起作用，形成了共享电子。其实电子的偶极-偶极作用，已经包含在及其复杂的电子相关计算之中了。

耦合簇等方法精确计算得到的电子密度形变图景的定向确定性，也不支持说范德华力无方向性、无饱和性这样的推测。

四、范德华力是卡西米尔效应吗？
从卡西米尔效应诞生之初，范德华力就被纳入卡西米尔效应体系，因为“瞬间偶极-偶极作用”静电吸引这样的思路，与卡西米尔效应有一致之处。荷兰物理学家Casimir 正是在进行范德华力有关的研究时, 在1948 年发表了一篇关于研究两块互相平行的中性导体板之间的吸引力的文章, 这种吸引力后来被称为卡西米尔(Casimir)力。
在正常情况下，真空中充满着几乎各种波长的粒子，如果使两个不带电的金属片紧紧靠在一起，较长的波长就会被排除出去，金属片外的其他波就会产生一种往往使金属片相互聚拢的力，金属片越靠近，两者之间的吸引力就越强，这种现象就是所谓的卡西米尔效应。

时至今天，范德华力与卡西米尔力都是实验证实客观存在的，它们也会有相互作用，但它们却不是同一个层次和范畴的。

首先、从作用的形式和距离看，卡西米尔力是两块互相平行的中性导体板之间的吸引力，其间的距离数量级在微米，而范德华力是原子（分子）之间的，距离数量级在几埃米，两者之间相差上千倍！在卡西米尔力作用的距离，根本不会形成范德华力。而在范德华力作用距离，也已经谈不上卡西米尔力，因为这时形成卡西米尔力的平行板早崩塌了。
其次、从作用能和作用力看，范德华作用能数量级在kJ∙mol^-1，而卡西米尔作用能数量级在J∙mol^-1，卡西米尔力数量级在10^-7牛顿。
第三、从基本表达式看，范德华力F∝1/r^7，r是原子间距。卡西米尔力F∝1/a^4，a为平行板间距。
第四、从势能随间距变化曲线看，范德华作用有一个能量的最低点的平衡距离，如果距离再加大，能量会缓慢上升；如果从这平衡距离再缩小，能量会急剧升高。而卡西米尔作用，只有随间距缩小体系合拢受力永远增大这样一种趋势。

总的说来，范德华力与卡西米尔力是不同层次、不同性质的两种力。
如果说范德华作用所形成的结合能比正常价键要小1～2个数量级的话，卡西米尔作用体系受力合拢能比范德华作用还要小2个数量级以上。
其实这二者在构成和性质上是完全不同的，本是没有可比性的。卡西米尔作用使体系受力合拢，只是数量上的变化，受外力合拢的体系本身材质不会有任何质的变化，这纯粹是个量子物理过程。而范德华作用所形成的结合由原子形成了分子、分子之间形成超分子，原子、分子发生了化学性质的变化，这种性质上的变化产生了范德华作用，这是个量子化学过程！

五、范德华作用量子化学图景的意义：
1、对范德华力的“电子的瞬间运动出现的瞬间偶极矩之间的作用” 的模型猜想，是仅用静电作用来解释范德华力，卡西米尔力更是在一定的格局下形成一种外力将材料挤拢，来解释范德华力，都脱离了量子化学。
这其实阻碍了对范德华力模拟、计算和研究。试想瞬间偶极矩如何度量、计算？并与实验测得的范德华作用距离、作用能相吻合？
这使得我们通常对化学课题进行量子化学精确计算研究、建立了模型图像之后，一涉及到弱相互作用的范畴，就只是用范德华力一言而敝之，心里想着它是瞬间偶极矩作用，并常常就此止步了，对范德华作用不能通过计算形成一个具体的形成机理、图景。

在量子化学看来，形成范德华力的双方电子是作为波在起作用的，而起作用的波是否合理，是用由它得到的电子密度分布安排是否合理来衡量的，而电子密度分布安排是要使得体系能量均衡（电负性均衡原理）、体系能量最低。

现在我们也动辄说电子密度、说电荷分布，但它们不是一种电荷模型设想，而是由量子化学计算的精细结果，电子是一个空间分布。范德华力是双方电子作为波相互作用之后的结果，包含了静电作用和电子相关，是内部起作用发生化学变化的结果，不是象卡西米尔力那样是在一定的格局之下，形成内外受力不均衡，由外力挤拢来形成结合力。也不是纯粹的静电引力作用，电子波的相互作用包含静电作用和电子相关，复杂得多。

2、现在我们看到了范德华作用的量子化学图景，它从成对电子的Pauli互斥开始，产生电子回避，形成了电子共享。我们不仅在惰性双原子准分子看到这种图景，而且对二体苯、二体叶绿素、生命分子的卷曲等等，都可以看到这种图景：电子排斥-回避-共享。
其实精确的量子化学计算早已经完全包含了这个范德华作用的图景，只是我们因为我们囿于传统经典的“瞬间偶极矩”作用模型，没有通过电子密度差来具体观察、分析而已。
可见只要选择的方法够好、基组合用，完全可以用来展现范德华作用的确切图景，研究范德华作用的具体过程和各种量值。吸附，催化，乃至化学反应等都是基于范德华作用而缘起、发生的。

3、现在有了以耦合簇为代表的量子化学方法，精确地考虑、计算了电子相关，从而也为我们树立了一个标杆。事实也正是这样，当Cybulski[3]用CCSD(T)/aug-cc-pV5z方法计算了He2，Ne2，Ar2，He-Ne，He-Ar，Ne-Ar的基态势能曲线，预测了平衡键长、解离能等之后，许多新的方法、基组的建立都与它相对照，判断是否可用。
现在对我们来说，对于一种量子化学方法，对于一组基组，以及它们是否配套，能不能用于研究我们的包含范德华作用的课题，我们可以在Gaussian09中用该方法/基组算一下惰性双原子准分子，并作出电子密度差，来与CCSD/aug-cc-pVTz算的密度差对照一下，就可以看出我们采用的方法/基组是否合用，合用的程度。并分析不合用的原因。
比如用CCSD/aug-cc-pVTz与CCD/aug-cc-pVTz作的电子密度差基本没有区别。但是对于MP4SDQ/cc-pVTz与MP4SDQ/aug-cc-pVTz，它们完全不相同，只有后者（加了aug）才能与CCSD/aug-cc-pVTz基本相符。

4、        要使用电子密度差方法来查看化学图景，这使得我们似乎看见了化学。
    现在用它研究各种化学体系的范德华作用。主要观察什么部位是排斥的中心，由于排斥电子又回避到什么部位了，在什么部位形成了什么样的共享电子图景。当然，如果涉及的是催化、化学反应，除了分析体系的范德华作用本身外，还要对体系优化结果，考察范德华作用引起的其他正常键的松动、变化，这里正是催化、化学反应的本源。

5、当然，根据耦合簇为代表的多种量子化学方法，精确地考虑、计算电子相关，得到的电子密度差图景，从而跟踪到的范德华作力形成的过程及本质，还需要进一步有更多的数据、事实来深入探讨和论证。特别是所谓共享电子，它有多少？是否足以维系着体系形成范德华作用的结合能，需要进一步数据确证。

6、物理有机，乃至化学，历来有多少经验的猜想、假说、原理，现在需要我们用严格的量子化学计算、图像来重新考察一下啊！ （2012/3/5）

[ Last edited by zhou2009 on 2012-3-6 at 09:31 ] 返回小木虫查看更多