| 查看: 2518 | 回复: 7 | |||
tian_an_men铁虫 (正式写手)
|
[求助]
关于量子光学中的哈密顿量问题。
|
|
想拓宽研究领域，对量子光学感兴趣，看了一些书籍，还是没有搞清楚，课本上和文献是怎样写出哈密顿量的。感谢大家不吝赐教！谢谢 具体如图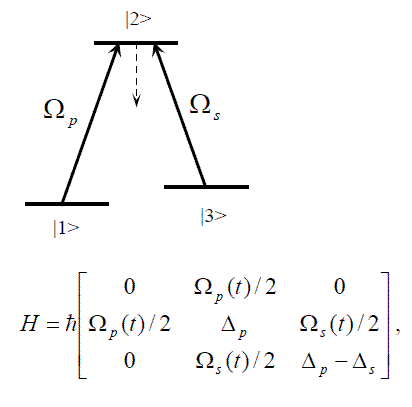：  怎样就把lamda 三能级的H 写成图中的形式？ 谢谢 [ Last edited by tian_an_men on 2011-8-10 at 10:40 ] |
回复此楼» 收录本帖的淘帖专辑推荐
 青椒不辣 辣椒不青 |
» 猜你喜欢
博士读完未来一定会好吗
已经有24人回复
-
导师想让我从独立一作变成了共一第一
已经有9人回复
-
到新单位后，换了新的研究方向，没有团队，持续积累2区以上论文，能申请到面上吗
已经有11人回复
-
读博
已经有4人回复
-
JMPT 期刊投稿流程
已经有4人回复
-
心脉受损
已经有5人回复
-
Springer期刊投稿求助
已经有4人回复
-
小论文投稿
已经有3人回复
-
申请2026年博士
已经有6人回复
» 本主题相关价值贴推荐，对您同样有帮助:
一维无限长原子链哈密顿矩阵怎么表示？
已经有6人回复- 看看如下哈密顿量如何进一步处理
已经有4人回复
- 关于量子的一点点体会，大家看看觉得对吗？
已经有20人回复
- 【求助】请教一个与自旋有关的哈密顿矩阵，锯齿形石墨
已经有4人回复
- 【交流】所有的二次型哈密顿量都能对角化吗？
已经有11人回复
- 【求助】关于光场量子化问题
已经有3人回复
tian_an_men
铁虫 (正式写手)
 |
2楼2011-08-10 10:41:28
racoon01
专家顾问 (著名写手)
-
专家经验: +213 - 物理EPI: 25
- 应助: 212 (大学生)
- 金币: 24354.4
- 散金: 27
- 红花: 71
- 帖子: 2438
- 在线: 643.2小时
- 虫号: 1282452
- 注册: 2011-05-01
- 专业: 中国近代史、现代史
- 管辖: 物理
3楼2011-08-10 21:13:51
tian_an_men
铁虫 (正式写手)
- 应助: 1 (幼儿园)
- 金币: 323.9
- 散金: 1712
- 红花: 2
- 帖子: 757
- 在线: 200.4小时
- 虫号: 929761
- 注册: 2009-12-17
- 专业: 原子和分子物理
4楼2011-08-11 00:13:59
racoon01
专家顾问 (著名写手)
-
专家经验: +213 - 物理EPI: 25
- 应助: 212 (大学生)
- 金币: 24354.4
- 散金: 27
- 红花: 71
- 帖子: 2438
- 在线: 643.2小时
- 虫号: 1282452
- 注册: 2011-05-01
- 专业: 中国近代史、现代史
- 管辖: 物理
5楼2011-08-11 07:52:04
gaorm
金虫 (小有名气)
- 应助: 3 (幼儿园)
- 金币: 1014.8
- 散金: 866
- 红花: 2
- 帖子: 194
- 在线: 142.9小时
- 虫号: 1579237
- 注册: 2012-01-16
- 性别: MM
- 专业: 凝聚态物性 II ：电子结构
6楼2012-02-16 01:21:20
7楼2012-02-17 18:37:01
8楼2021-12-22 18:44:30