| 查看: 3571 | 回复: 7 | |||
eastnobil铁虫 (初入文坛)
|
[交流]
【求助】gamma点指的是什么？已有4人参与
|
| 常常见文献里用gamma点的态密度或者电荷密度来分析和说明问题，那么这里的gamma点指的是什么？实空间的平面还是点？ |
回复此楼» 猜你喜欢
2025冷门绝学什么时候出结果
已经有6人回复
-
Bioresource Technology期刊，第一次返修的时候被退回好几次了
已经有7人回复
-
真诚求助：手里的省社科项目结项要求主持人一篇中文核心，有什么渠道能发核心吗
已经有8人回复
-
寻求一种能扛住强氧化性腐蚀性的容器密封件
已经有5人回复
-
请问哪里可以有青B申请的本子可以借鉴一下。
已经有4人回复
-
请问下大家为什么这个铃木偶联几乎不反应呢
已经有5人回复
-
请问有评职称，把科研教学业绩算分排序的高校吗
已经有5人回复
-
天津工业大学郑柳春团队欢迎化学化工、高分子化学或有机合成方向的博士生和硕士生加入
已经有4人回复
-
康复大学泰山学者周祺惠团队招收博士研究生
已经有6人回复
-
AI论文写作工具：是科研加速器还是学术作弊器？
已经有3人回复
» 本主题相关价值贴推荐，对您同样有帮助:
帮忙求个向量函数的极限
已经有3人回复- EST标签的这个“标签”指的是什么？
已经有4人回复
- physical review b 的引用文献格式
已经有3人回复
- 滤波器的模板宽度指的是什么？
已经有5人回复
- "4次跨膜蛋白"中的“4次”指的是什么？
已经有3人回复
- Zview中各元件代码指的是什么？
已经有9人回复
- 在研材料指的是什么？
已经有8人回复
- gamma-Fe2O3是什么颜色？
已经有4人回复
- 【求助】OD材料指的是什么材料
已经有4人回复
- 求教个专业术语：酶的催化位点和活性位点各指的是什么意思
已经有6人回复
- sacrificial agent指的是什么？求教
已经有7人回复
- 非gamma点处的虚频意味着什么？
已经有14人回复
- 【求助】能带结构中Gamma点的特征是怎么求出来的？
已经有3人回复
- 【求助】有关马氏体的Md点指的是什么？
已经有5人回复
- 【求助】gamma Al2O3建模
已经有5人回复
- 请教大家一个问题:液体的压力p到底指的是什么
已经有7人回复
2楼2010-04-04 16:49:43
eastnobil
铁虫 (初入文坛)
- 应助: 0 (幼儿园)
- 金币: 169.5
- 帖子: 13
- 在线: 21.3小时
- 虫号: 740034
- 注册: 2009-04-04
- 专业: 凝聚态物性 II ：电子结构
3楼2010-04-04 16:51:32
4楼2010-04-05 10:29:56
eastnobil
铁虫 (初入文坛)
- 应助: 0 (幼儿园)
- 金币: 169.5
- 帖子: 13
- 在线: 21.3小时
- 虫号: 740034
- 注册: 2009-04-04
- 专业: 凝聚态物性 II ：电子结构
★ ★
tongling921(金币+2):3x 2010-04-05 22:20
tongling921(金币+2):3x 2010-04-05 22:20
|
谢谢精彩的回答，受教了。 可是我的疑问又不禁产生，如果这个gamma点与实空间没有一个一一对应的关系,为何文献中常见对gamma点的实空间分析呢，举几个例吧(google中用关键词"charge density of gamma point"搜索得到)： 第一个 网址：http://jolisfukyu.tokai-sc.jaea. ... ai-en/2007/4_3.html 里面出现了这样的一个图  对（e）图的说明是：(e):LO-mode at Γ-point(shown in 3D) 第二个 文献：Okada, S. and A. Oshiyama (2003). "Curvature-induced metallization of double-walled semiconducting zigzag carbon nanotubes." Physical Review Letters 91(21): 216801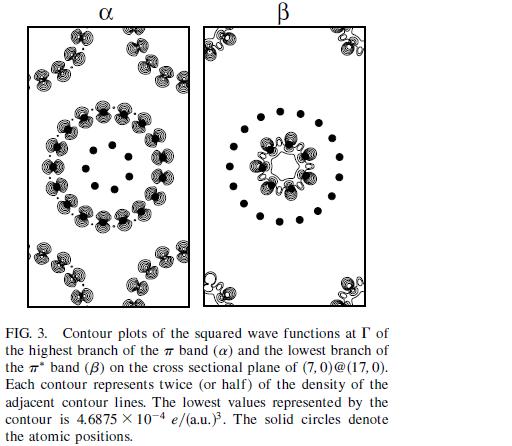. 里面的图3  第三个 文献：Charlier, J. C., P. Lambin, et al. (1996). "Electronic properties of carbon nanotubes with polygonized cross sections." Physical Review B 54(12): R8377-R8380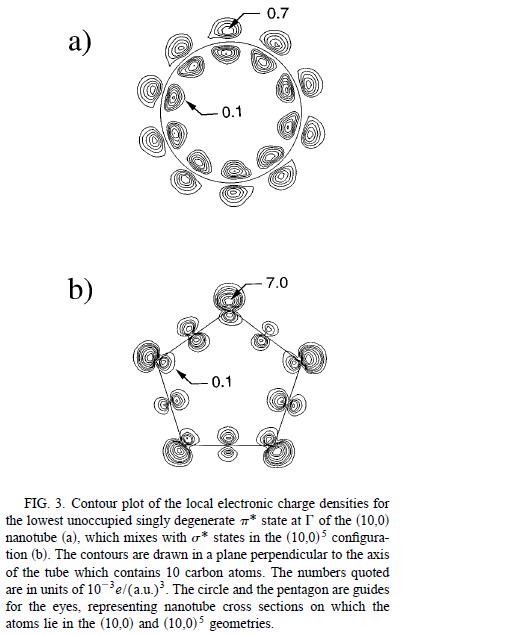. 也是图3  |
5楼2010-04-05 13:58:13
★ ★
小木虫(金币+0.5):给个红包，谢谢回帖交流
tongling921(金币+1):3x 2010-04-05 22:21
小木虫(金币+0.5):给个红包，谢谢回帖交流
tongling921(金币+1):3x 2010-04-05 22:21
|
你给的第一个例子里k可以用来描述晶格原子的运动状态，这个时候波矢k对应的是晶格原子振动构成的集体状态,而所有这些k都在第一布里渊区内，原点gamma点对应的就是，集体振动状态波长为无穷长的一个状态(以一维链为例，所有primitive cell里的A原子同一时刻相对于原来平衡位置的位移是一样的，就他们整体的行为来看这就是波长无穷长的极限情况。由于实空间原子集体振荡的波长不能小于晶格常数a,但可以趋于无穷大（理想情况），所以在倒易空间来考虑，k不能大于第一布里渊区，但可以趋于0)。 后面两个例子考虑的是系统电子波函数（Bloch）函数有一个波矢k,这个k可以取在第一布里渊区内，原点即为gamma点，k是波函数的量子数的标志。和上一个例子有点类似。但这里说的是当你体系波函数处在Bloch波矢为k=0（at gamma point）的量子数的时候，你体系在实空间电荷分布是个什么样子的~ 总之吧，后面这里的gamma point都是描述体系的一个状态，考虑的已经不再是简单的规则排列静止的晶格了，这里考虑的是新的自由度，而不再是简单的晶格点阵实空间与倒易空间简单的对应~ |
6楼2010-04-05 15:42:41
好 |
7楼2011-03-04 11:31:33
夕阳西下
金虫 (著名写手)
- 应助: 138 (高中生)
- 贵宾: 0.041
- 金币: 9247.1
- 散金: 73
- 红花: 28
- 沙发: 1
- 帖子: 1268
- 在线: 1164.4小时
- 虫号: 220750
- 注册: 2006-03-20
- 专业: 凝聚态物性 II ：电子结构
- 管辖: 物理
8楼2011-03-04 14:03:17