|
|
【答案】应助回帖
边学习,边回答这个问题。
工具:用Mathematica 解决。求解这类问题,Mathematica首屈一指。
首先是描述两条曲线的代码:
上面代码定义各个常数,以及两条曲线的参数方程。因为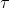 并不是一个自然的参数,需要计算曲线封闭的情况下实际的周期是多少,算出来是 并不是一个自然的参数,需要计算曲线封闭的情况下实际的周期是多少,算出来是  ; 并显示根据对称性和Green定理需要求解的1/10图形的样子 ; 并显示根据对称性和Green定理需要求解的1/10图形的样子
然后用Green定理计算转子曲线的面积:
结果是:
6557.97718280445
现在开始求已知面积是 6557.19 时的  , 需要先把面积表示成 , 需要先把面积表示成  的函数,其它参数都不变; 然后用牛顿法迭代: 的函数,其它参数都不变; 然后用牛顿法迭代:
我的电脑比较破,用的时间很久, 结果是:
用时间172.41342746027159秒,
对应的 
要不是误以为楼主是另外一位同学,我也许就不来解这道题了。不过,总算解完了。希望楼主能够举一反三。 |
|

















 回复此楼
回复此楼

 丫头丫头2014
丫头丫头2014