应《网络安全法》要求，自2017年10月1日起，未进行实名认证将不得使用互联网跟帖服务。为保障您的帐号能够正常使用，请尽快对帐号进行手机号验证，感谢您的理解与支持！

24小时热门版块排行榜    

小木虫论坛-学术科研互动平台 » 计算模拟区 » 分子模拟 » LAMMPS/DL_POLY » 【分享】尝试lammps中, 分享中...
52/1返回列表
查看: 5888  |  回复: 15
只看楼主 @他人 存档 新回复提醒 (忽略) 收藏    在APP中查看
本帖产生 2 个 模拟EPI ，点击这里进行查看
当前只显示满足指定条件的回帖，点击这里查看本话题的所有回帖

qphll

金虫 (正式写手)

[交流] 【分享】尝试lammps中, 分享中... 已有9人参与

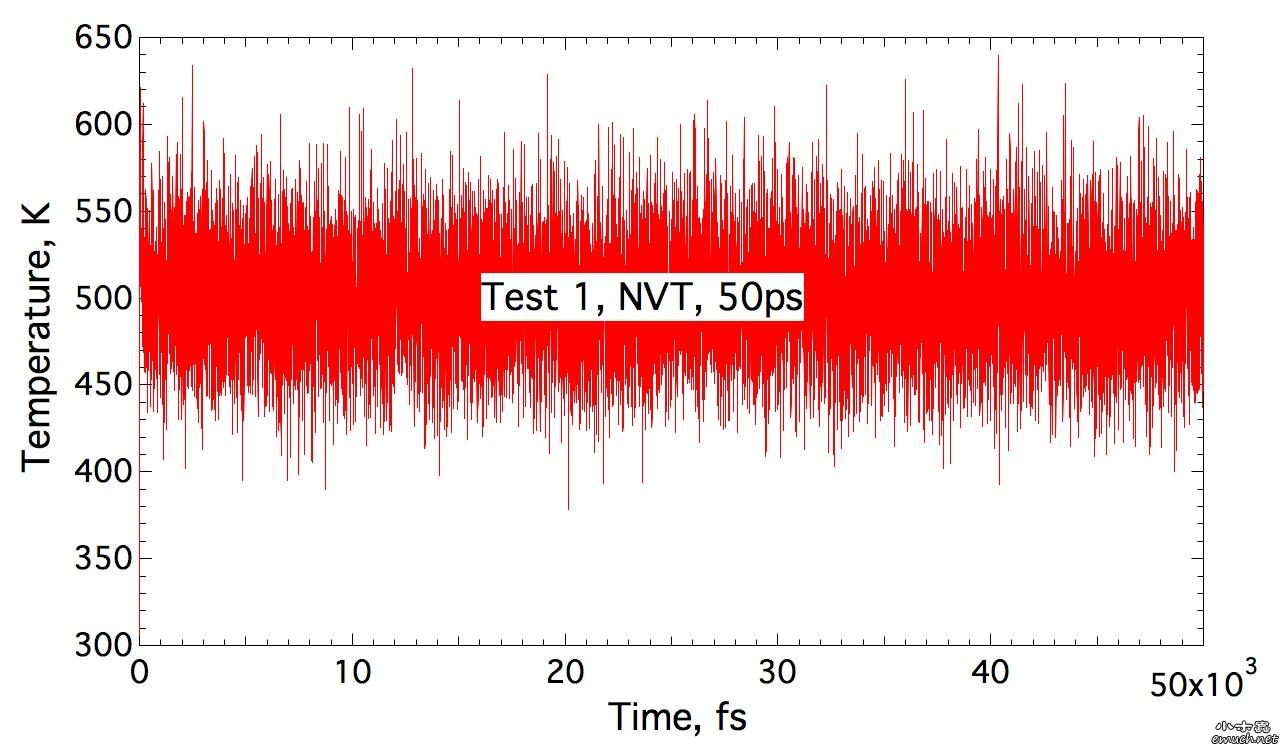
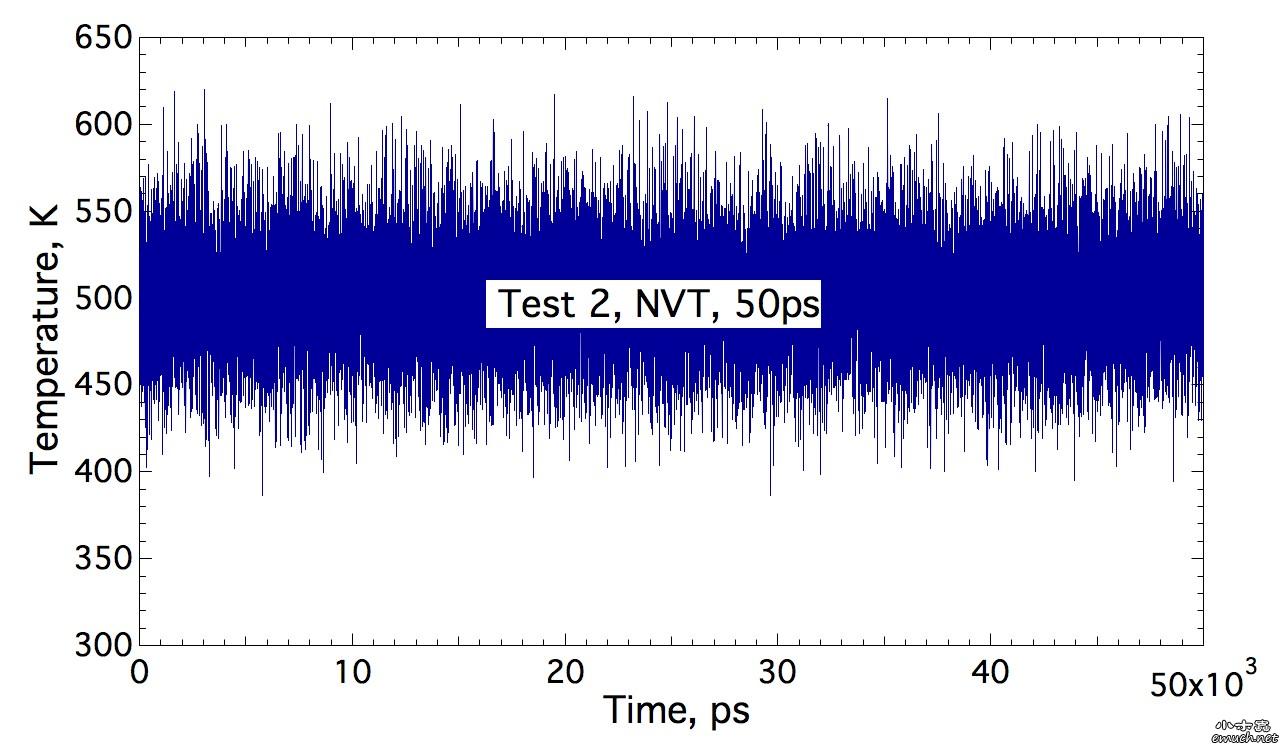
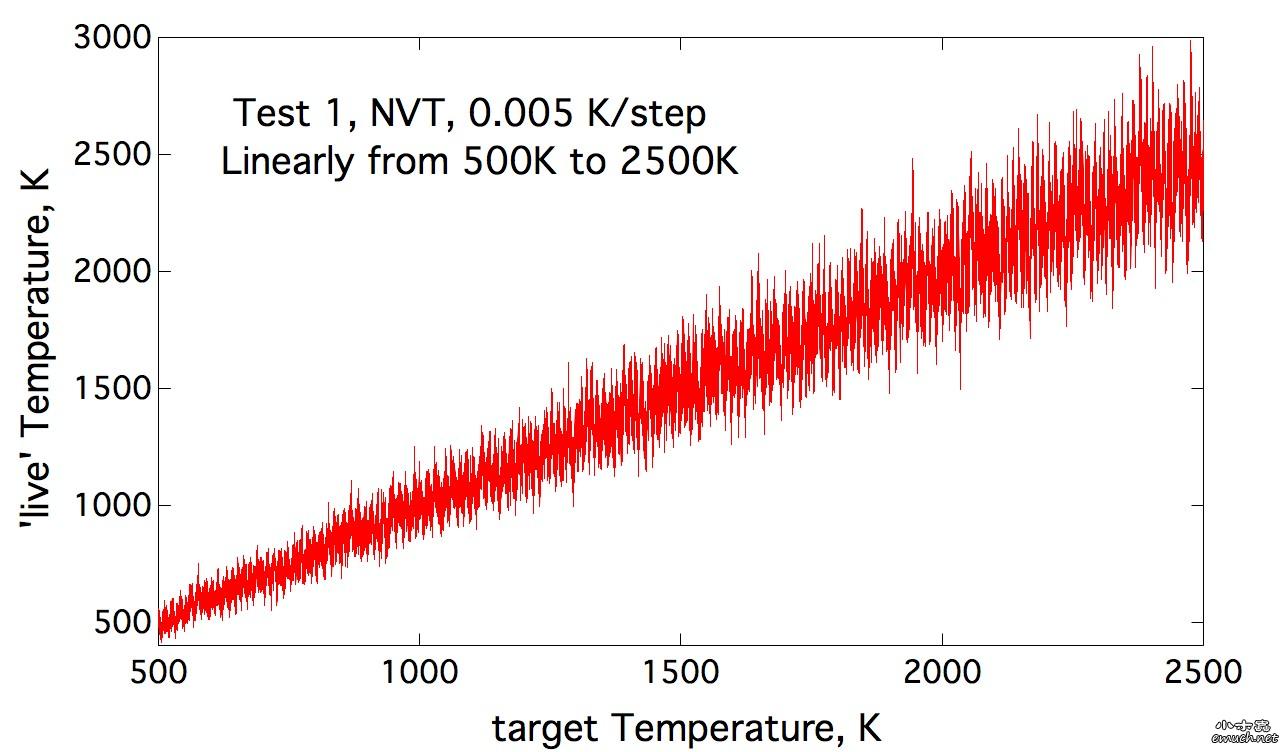
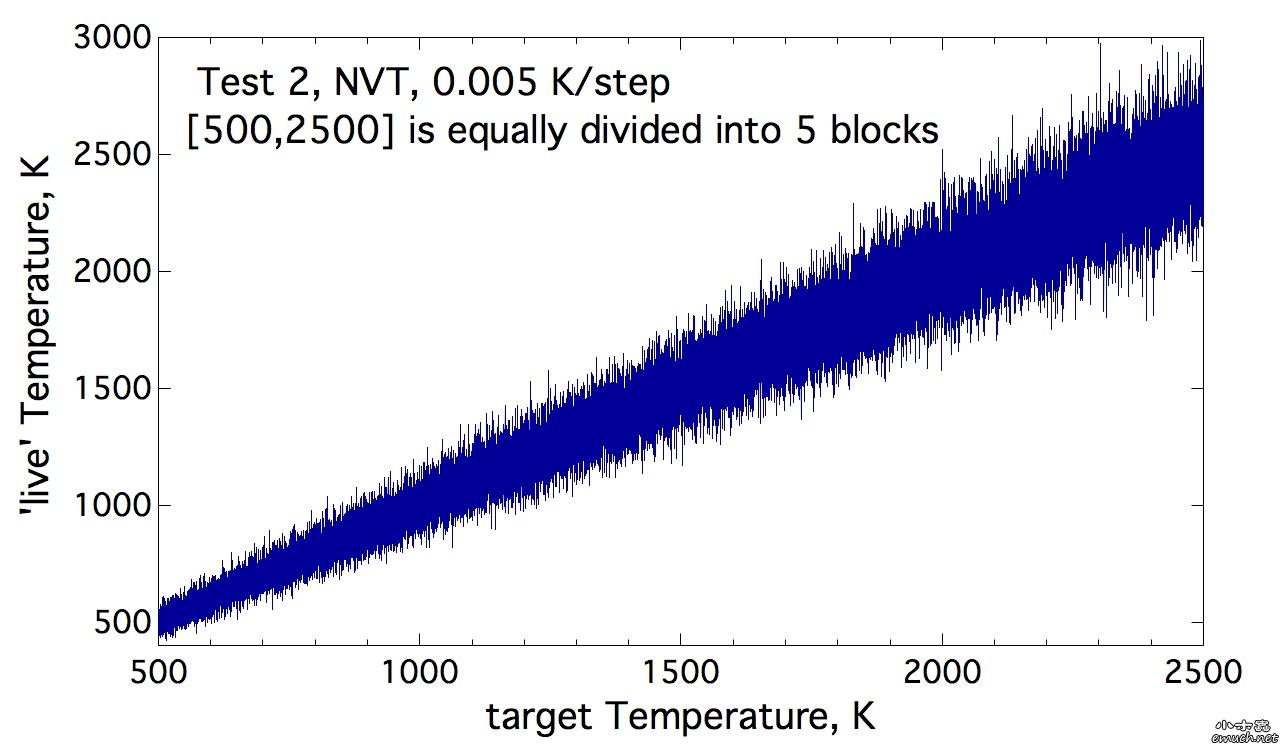
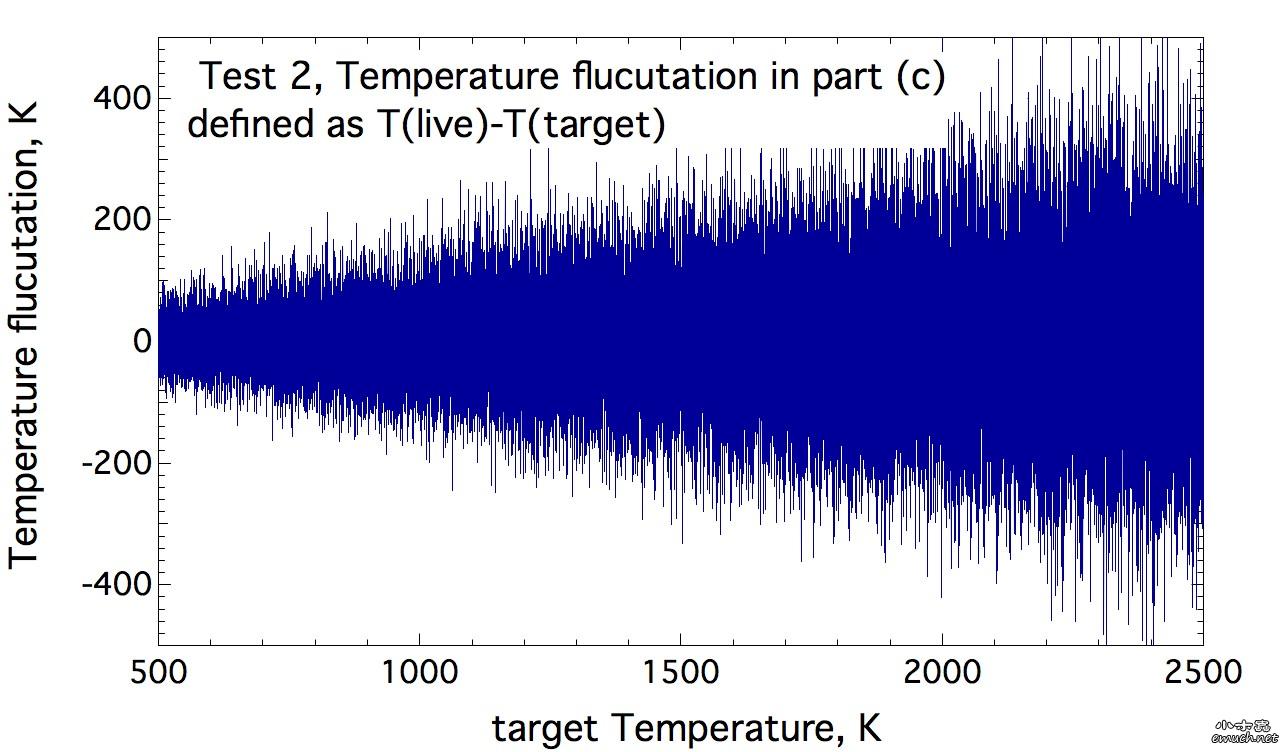
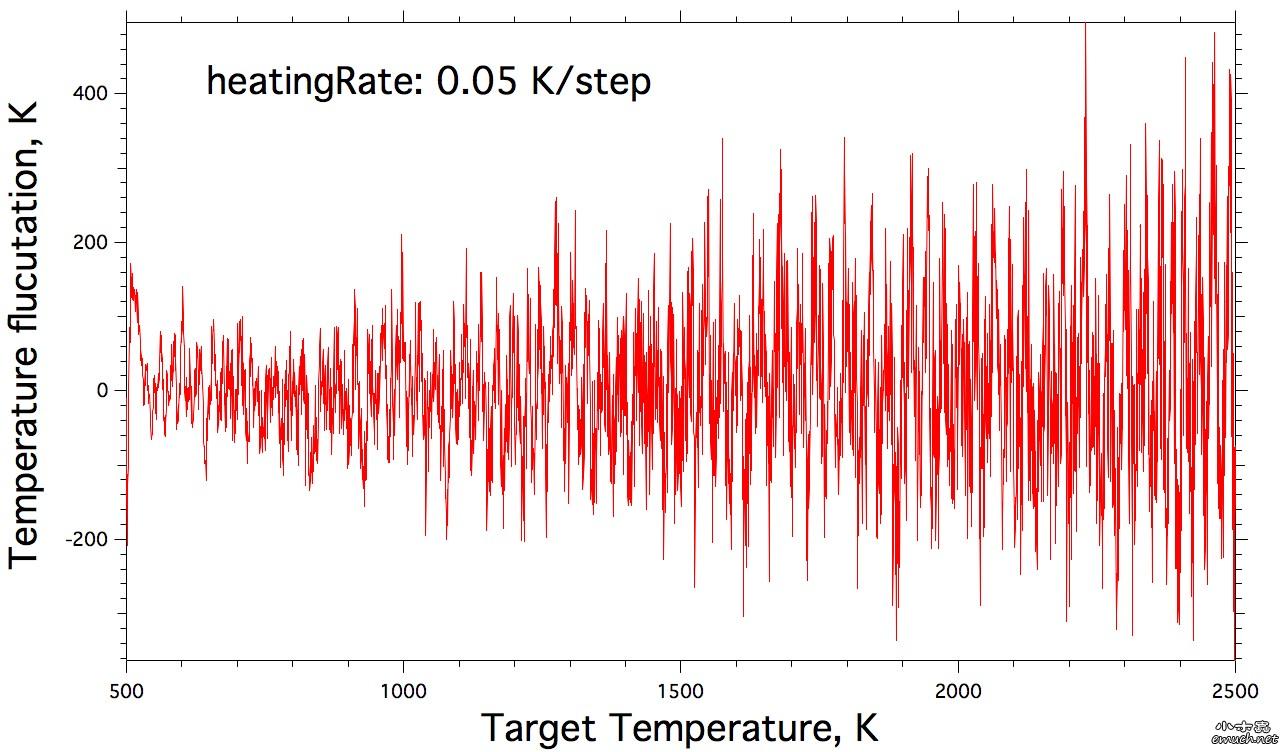
Lesson 1
Loop inside Lammps input script


想要尝试在lammps的input script里面做循环, 结果因为一个小问题, 捣鼓了我几个小时, 这才完全通过测试. 分享一下.


(1) input script里面的循环块

include tempfile
include tempfile2

variable i loop 10
label loopa
       fix 2 all nvt temp ${mytemp} ${mytemp2} 100.0
        run 200
        unfix 2

       next mytemp
       next mytemp2
next i
jump SELF loopa

这个的SELF是让程序执行到这里, 跳回自己, 然后从标签 loopa开始执行. 当然loopa是随便取的, 你可以用CHN来做label.

另外, 在某些情况下, 如果要让c++ rewind, 那么最好在执行脚本里面这样写:

lmp -in script

而不是

lmp < script

否则, 你人品不好的时候, 会出问题, 哈哈.


(2) tempfile 和 tempfile2是在同目录下的另外两个文件. tempfile的文件内容是:

variable mytemp index 500.0 700.0 900.0 1100.0 1300.0 1500.0 1700.0 1900.0 2100.0 2300.0

注意, 只有一行!  至于lammps能读多长的一行, 我还没有测试.


tempfile2的文件内容, 也是一行:

variable mytemp2 index 700.0 900.0 1100.0 1300.0 1500.0 1700.0 1900.0 2100.0 2300.0 2500.0

折腾我的问题是, 我原先在这两个tempfile文件中, 数值之间用逗号分隔, 但是事实上, 是需要用空格分隔的.

(3)  如果你需要做的循环不是很多, 那么不需要额外准备tempfile 和 tempfile2文件. 而只是需要在 input script中这样做:

variable mytemp index 500.0 700.0 900.0 1100.0 1300.0 1500.0 1700.0 1900.0 2100.0 2300.0
#variable mytemp2 index 700.0 900.0 1100.0 1300.0  1500.0 1700.0 1900.0 2100.0 2300.0 2500.0

variable i loop 10
label loopa
       fix 2 all nvt temp ${mytemp} ${mytemp2} 100.0
        run 200
        unfix 2

       next mytemp
       next mytemp2
next i
jump SELF loopa

当然, 这里不需要原先的这两句 include语句了.


总结一下你需要熟悉的命令:

variable, include, jume, next


End of Lesson 1.

ENJOY.

[ Last edited by qphll on 2010-12-3 at 11:54 ]
回复此楼

» 本帖已获得的红花（最新10朵）

fly771125 生与死后

» 猜你喜欢
Life, Love, Laugh.
1楼 2010-12-03 11:43:29
已阅   回复此楼   关注TA 给TA发消息 送TA红花 TA的回帖

1040720479

新虫 (小有名气)
★
小木虫: 金币+0.5, 给个红包，谢谢回帖
引用回帖:
7楼: Originally posted by qphll at 2010-12-11 10:32:02
前面的两个版本, 还是不满意.

Lammps作者给的c代码,也是不满意.

自己写, 想了一天了, 也还是不满意.

忽然发现现在的主要的问题是: 我想从计算的结果中分析什么?!

加油, 加油.

贴出Lammps 的Adian给 ...

楼主请问一下，我的species里只有一个大的分子团，我需要在哪里修改cutoff呢？fix species的cutoff又有什么意义?bond文件内生成的是否是真实的键级？如果有相关的资料可以深入学习自当感激不尽！
赞一下 回复此楼
16楼2020-12-03 19:59:49
已阅   回复此楼   关注TA 给TA发消息 送TA红花 TA的回帖
查看全部 16 个回答

qphll

金虫 (正式写手)
★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★
ghcacj(金币+20):谢谢 2010-12-04 17:09:24
Lesson 2 Reax FF

就不自己翻译成中文了吧, 反正大家都能看明白的. 拼写错误啦, 语法错误啥的, 大家多包涵就是了.

如果核心内容上, 对于原理的理解上有任何错误的, 请指出.


Two tests have been carried out for NH3_Graphene_COOH_OH systems. The same initial.dat and ffielf.reax files are used. Timestep is 0.25 fs and initial velocities are generated according to Maxwell-Boltzmann distribution.

The only difference is the heating up procedure.

Test 1:

(a)        Minimize the initial structure;
(b)        Run 200000 steps (50 ps) to equilibrate the system, NVT ensemble with the damping parameter at 10.0;
(c)        Heat up the system linearly from 500K to 2500K at the rate of 0.005 K/step, NVT ensemble with the damping rate of 10.0.

Test 2

(a)        Minimize the initial structure;
(b)        Run 200000 steps (50 ps) to equilibrate the system, NVT ensemble with the damping parameter at 1.0;
(c)        Divide the temperature range of (500, 2500) into 5 blocks, and heat up the system linearly in each block and continuously between blocks. The rate is still 0.005 K/step, NVT ensemble with the damping rate of 1.0.

Here are the results and figures.

Figure 1 Temperature vs. simulation time, part(b), NVT ensemble.

The temperature damping parameter is 1.0 for test 1 and 10.0 for test 2. Generally, temperature can fluctuate wildly if the damping parameter is too small, while on the other hand, too large damping parameter will take a very long time to equilibrate the whole system. I may do more tests to get the optimized value for this temperature damping parameter.


Figure 1





Figure 1. Temperature vs. simulation time, the NVT ensemble at step (b).







Figure 2. ‘live’ Temperature vs. target Temperature, part (c), NVT ensemble.







Figure 3. Temperature fluctuation vs. target Temperature.



The reason for the blocks in test 2 is that, I was planning to do some NVE between each NVT iteration, hoping that could bring forth the better control over the system temperature. So in the Lammps input script, part (c) is being taken care of by the following commands:

Test 1:

fix 2 all nvt temp 500.0 2500.0 10.0
run 400000

Test 2:

variable mytemp index 500.0, 900.0, 1300.0, 1700.0, 2100.0
variable mytemp2 index 900.0, 1300.0, 1700.0, 2100.0, 2500.0
label loopa
variable i loop 5
       fix 2 all nvt temp ${mytemp} ${mytemp2} 1.0
       run 80000
       unfix 2
       next mytemp
       next mytemp2
next i
jump in.reaxff loopa

There are two other issues here. One is that I realize the temperature of first step of part (c) is not exactly 500.0K. This is because the NVT of part (b) cannot bring in 500.0K as the temperature of its final output.  Does it mean that part (b) is actually not necessary?

The other is that I am not sure I completely understand the philosophy of temperature programmed reaction method.

Here are my thoughts of the whole process:

Minimization is necessary to make sure you don't have any overlaps.  Then when you add temperature (give your atoms velocities) your system won't blow up. Once the temperature (atomic velocity) has been assigned, you first should use a thermostat to equilibrate the system.  This can be a Berendsen or a Langevin, depending on what you want to do, as these have a random term in them and this helps to equilibrate faster.

But if you want to measure dynamics at a constant temperature, you should use NVE.  However, you want to alter the temperature and measure (or follow) the dynamics, so in this I would use a Nose-Hoover thermostat (fix temp/nvt).
That is why I break the whole process into three parts as I describe previously:


(1) Use minimization to minimize the structure (from my test run, it seemed that the initial structure is already pretty close to a local minimum, as the search stopped after 169 steps or so);

(2) Use a thermostat (Berendsen or Langevin) to equilibrate the temperature.  You could also use a Nose-Hoover here as well and I think it would be ok.  The Berendsen or Langevin thermostat would likely get you there faster.

(3) Use a thermostat to ramp up the temperature from 500 K to 2500 K.
Here I would use a Nose-Hoover thermostat since I have a pretty small system.  So if I use a Berendsen or a Langevin thermostat, I would have to use a large damping parameter here and the results likely would not be realistic.  If I use a small damping parameter, the results would be better for the dynamics but the temperature control would not be very good.  So a Nose-Hoover with a reasonable damping parameter is probably the best. That is what I use in part (c):

fix 2 all nvt temp 500.0 2500.0 10.0

Of course I then need to find that reasonable damping parameter.
If we could manually do several iterations at the very beginning of part (C), let’s see what happens there:

(a)        Image 1, t=0, T(target)=500K, we assign the atomic velocities at 500K. With atomic positions and force field, we know the forces on each atom and thus the acceleration. Do one iteration by Verlet algorithm to go to step 2.
(b)        Image 2, t= 0.25fs, T(target)=500.005K, from (a) we get the velocities at this step 2, new coordinates, new forces and new accelerations. The real temperature can be calculated at this step and rescaling (of atomic velocities) is applied by Nose-Hoover algorithm to bring the real temperature to the target temperature 500.005K. Use the rescaled velocities to go a step further to image 3.
(c)        Keep doing this time integration and controlling over temperature to do the temperature ramp up steadily along the way.

By increasing temperature slowly and steadily, each atom possess more total energy (potential and kinetic), and make it possible to overcome the energy barriers such as bonds, angles, and even Pi-Pi interaction, and thus old-bond breaking and new-bond forming is more and more possible along the way. Also, from this point of view, there is no advantage of dividing the temperature range into several block.


THE MOST SERIOUS PROBLEM is:
From Figure 3, we can see large fluctuation at high temperature. Is that acceptable? If not, how can we bring down the fluctuation?
赞一下(1人) 回复此楼
Life, Love, Laugh.
2楼2010-12-04 15:07:09
已阅   回复此楼   关注TA 给TA发消息 送TA红花 TA的回帖

sg18408926

至尊木虫 (著名写手)
太好了，正在学习中
赞一下 回复此楼
3楼2010-12-04 17:27:08
已阅   回复此楼   关注TA 给TA发消息 送TA红花 TA的回帖

qphll

金虫 (正式写手)
★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★
ghcacj(金币+20):谢谢 2010-12-10 10:40:58
I am sharing some other test output with you.

reax FF, Lammps, Temperature Programmed Reax MD


(1) The NVT damping parameter of Lammps

The tests were carried out for 10 different values of that damping coefficients. I find that changing that parameter could not bring forth better control of temperature during the whole damping process. The flucutation is reduced a little bit at some value. But generally I would say there is no pointing of doing this type of parameter optimizaiton.

(2) Heating rate

With a same timestep of 0.25 fs, I tried the different heating rate from 500K to 2500K, namely, 0.01 K/step, 0.05K/step and 1 K/step. From the attached temperature flucutation plots, I observed (a) changing the rate from 0.005 K/step to 0.01 K/step or 0.05 K/step does not change much of the temperature flucutation. Does is mean that we could heat up the system faster? Or we do have very good reason in using the heating rate of 0.005 K/step? (b) at lower rate (0.005 K/step, 0.01 K/step and 0.05 K/step), it is not easy to control the temperature flucutation.  But at 1 K/step, compared with the other three rates, the fluctuation looks smooth for [900K, 1800K]. It may comes from fewer statistic points, but is it worthy of trying different heating rates for low temperature, median temperature and high temperature?

0.01 K/step



0.05 K/step



1 K/step





I do not think those tests are going to change anything about the TPRD procedures. They are just my thoughts when I am collecting the outputs.
赞一下(1人) 回复此楼
Life, Love, Laugh.
4楼2010-12-07 23:19:38
已阅   回复此楼   关注TA 给TA发消息 送TA红花 TA的回帖
查看全部 16 个回答
普通表情 龙 兔 虎 猫 高级回复 (可上传附件)
信息提示
关闭
请填处理意见
关闭