| 查看: 3860 | 回复: 16 | |||
| 当前只显示满足指定条件的回帖，点击这里查看本话题的所有回帖 | |||
[求助]
二元函数可微和可导的区别 已有3人参与
|
|||
|
二元函数可导的条件是什么啊？哪位大神知道，求告知 发自小木虫Android客户端 |
回复此楼» 猜你喜欢
表哥与省会女结婚，父母去帮带孩子被省会女气回家生重病了
已经有12人回复
-
依托企业入选了国家启明计划青年人才。有无高校可以引进的。
已经有14人回复
-
江汉大学解明教授课题组招博士研究生/博士后
已经有3人回复
-
AI 太可怕了，写基金时，提出想法，直接生成的文字比自己想得深远，还有科学性
已经有11人回复
-
依托企业入选了国家启明计划青年人才。有无高校可以引进的。
已经有11人回复
alober
木虫 (著名写手)
- 数学EPI: 1
- 应助: 18 (小学生)
- 金币: 22815.2
- 红花: 25
- 帖子: 2681
- 在线: 473.6小时
- 虫号: 3331731
- 注册: 2014-07-20
|
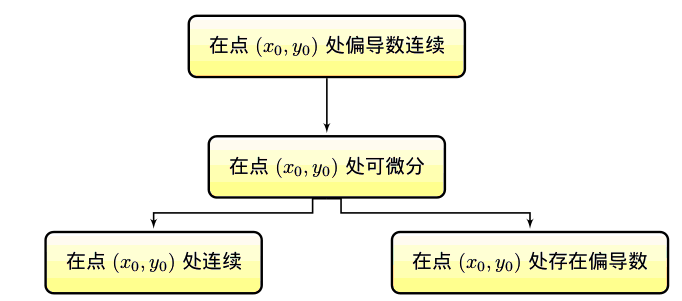
\begin{tikzpicture}[node distance=1cm, auto] \tikzset { node_box/.style={rectangle,rounded corners,draw=black, top color=white, bottom color=yellow!50,very thick, inner sep=1em, minimum size=3em, text centered}, arrow_box/.style={->, >=latex', shorten >=1pt, thick}, label_box/.style={text width=7em, text centered} } \node[node_box] (c-1) {在点$(x_0,y_0)$处偏导数连续}; \node[node_box, below=of c-1] (c-2) {在点$(x_0,y_0)$处可微分}; \node[below=of c-2] (dummy) {}; \node[node_box, left=of dummy] (c-3) {在点$(x_0,y_0)$处连续}; \node[node_box, right=of dummy] (c-4) {在点$(x_0,y_0)$处存在偏导数}; \draw[arrow_box] (c-1.south) -- (c-2.north); \draw[arrow_box] (c-2.south) -- ++(-.25,0) -- ++(0,-.25) -| (c-3.north); \draw[arrow_box] (c-2.south) -- ++(.25,0) -- ++(0,-.25) -| (c-4.north); \end{tikzpicture} 如上。不知道论坛能不能正确显示，还不太会用这个论坛。这段代码在tikz论坛也有示例，我照着改过来的。 |
14楼2016-10-31 20:10:56
hylpy
专家顾问 (知名作家)
唵嘛呢叭咪吽
-
专家经验: +2500 - 数学EPI: 7
- 应助: 381 (硕士)
- 贵宾: 0.167
- 金币: 51119.8
- 散金: 5568
- 红花: 410
- 帖子: 5093
- 在线: 1102.4小时
- 虫号: 3247778
- 注册: 2014-06-01
- 性别: GG
- 专业: 函数论
- 管辖: 数学
2楼2016-10-29 18:16:57
alober
木虫 (著名写手)
- 数学EPI: 1
- 应助: 18 (小学生)
- 金币: 22815.2
- 红花: 25
- 帖子: 2681
- 在线: 473.6小时
- 虫号: 3331731
- 注册: 2014-07-20
3楼2016-10-30 08:14:04
alober
木虫 (著名写手)
- 数学EPI: 1
- 应助: 18 (小学生)
- 金币: 22815.2
- 红花: 25
- 帖子: 2681
- 在线: 473.6小时
- 虫号: 3331731
- 注册: 2014-07-20
4楼2016-10-30 08:14:54